Um corpo de massa movimenta-se dentro de um funil descrevendo uma trajetória circular de raio , com velocidade de módulo constante. A superfície laterial do funil, de atrito desprezível, faz um ângulo com a vertical como mostrado na figura. Sendo o módulo da força que a superfície faz sobre o corpo, sua velocidade será dada por
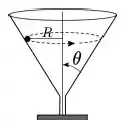
Passo 1
Bora lá, pessoinhas da melhor faculdade desse Brasil?
Questão de movimento circular e força te lembra o que? Isso, força centrípeta!
Bom, como vamos chegar a essa velocidade? Vamos usar a força centrípeta que age no corpo, afinal de contas, ele está girando.
E como vamos chegar nessa força centrípeta. Primeiro devemos pensar nas forças que estão agindo no corpo: A força peso e a normal que a superfície faz no corpo. Ou seja:
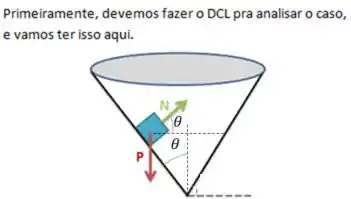
Bom, a força peso age na vertical, não temos como decompor ela pra achar a força centrípeta( que nesse problema fica na horizontal.
Resta a força normal. Se liga como vamos decompor essa força. Primeiro precisamos achar o ângulo que a normal faz com a horizontal:
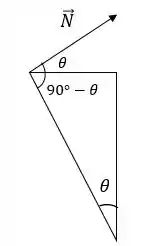
A partir daí, vemos que a forças normal se divide nas componentes abaixo:
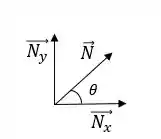
Assim:
E é essa a componente que gera a força centrípeta.
Agora a gente iguala essa componente da normal com a força centrípeta !!
Isolando o nosso vezinhu
Resposta
Letra A