Uma vasilha de massa muito grande permanece sempre em repouso sobre uma mesa horizontal (a mesa não é mostrada na figura). A forma da vasilha é a de um tronco de cone circular reto com base de raio igual a e superfície lateral que faz um ângulo com a mesa. Deslizando por sua superfície interna sem atrito, um pequeno bloco de massa descreve um movimento circular uniforme de velocidade no sentido indicado pela flecha e sempre à mesma altura . No sistema de coordenadas mostrado, o plano - é horizontal e a gravidade é dada pelo vetor .
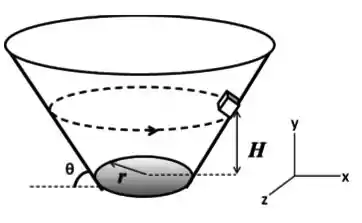
a) Num dado instante, a velocidade do bloco é dada pelo vetor . Represente o diagrama de corpo livre para o bloco nesse instante e desenvolva a segunda lei de Newton para cada um dos três eixos, , , . Encontre também o raio de curvatura da trajetória do bloco, em função de , e .
b) Considere , , , . Para uma trajetória do bloco com raio de curvatura , encontre o módulo da velocidade e o vetor que representa a força normal de contato exercida pela vasilha sobre o bloco.
c) Marque somente uma opção. Não é necessário justificar. No mesmo instante em que a velocidade do bloco é dada pelo vetor , a mesa exerce sobre a vasilha uma força total designada pelo vetor: . Sobre este vetor, é correto afirmar:
(i);
(ii);
(iii);
(iv);
(v);
(vi)
Passo 1
(a)
O vetor velocidade estará no sentido de na posição indicada na figura, logo as forças atuantes serão a força peso e a normal:
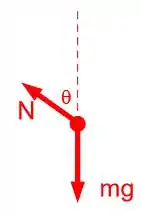
Aplicando a segunda lei de Newton para o bloco, lembrando que a força resultante é a centrípeta apontando para o centro do circulo e de fórmula :
Eixo x:
Eixo :
Eixo :
Raio de curvatura, :
Onde forma-se um triângulo de catetos e que podem ser relacionados por:
Substituindo no raio da curvatura:
Passo 2
(b)
Dividindo a equação do eixo () pela equação do eixo ():
Substituindo os dados:
As componentes da normal ficam:
Finalmente:
Passo 3
(c)
Essa força resultante que o recipiente exerce no bloco é justamente a força normal que calculamos no item anterior:
Ou seja, a componente é menos que zero, a componente é maior que zero e a componente é igual a zero.
Alternativa iii
Resposta
(a)
(b)
(c) Alternativa iii