Os pneus de um carro de massa têm coeficiente de atrito estático com a pista horizontal de uma rodovia em uma curva circular de raio . A velocidade máxima com que o corpo pode fazer essa curva sem derrapar é . Supondo que o carro faça a curva com velocidade de módulo constante , podemos dizer que, nesse caso, a força de atrito estático entre os pneus e a pista tem módulo igual a
Passo 1
Vamos começar analisando o movimento com velocidade
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Não, não existe um fio atuando.
Não, não existe mola atuando.
Sim, existe atrito.
A grande dúvida é para onde ficara o atrito?
Nesse problema se consideramos apenas o peso e a normal teremos forças na vertical, a curva é feita na horizontal, então a curva é feita pela força de atrito. Isso nós diz que a força de atrito aponta para o centro da curva.
OBS:
A força de atrito de uma roda com uma superfície não é considerada a força de atrito dinâmica, mas sim a força de atrito estática. Por quê? Porque a roda não está arrastando no chão, mas sim tocando nele.
O DCL do carro fica
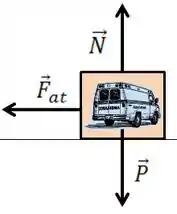
Passo 2
A força de atrito é a única força que atua na direção do centro da curva logo
A força centrípeta na primeira situação é
Então
Passo 3
Quando mudamos o movimento, o DCL fica exatamente igual, porém mudandando a velocidade iremos mudar a força centrípeta, e conseqüentemente a força de atrito. Ainda teremos
Vamos calcular a com a nova velocidade
Então
É importante entender que a força de atrito estática NÃO é dada pela fórmula. O que a fórmula nos diz é a força de atrito MÁXIMA.
Resposta
Letra B