Uma pequena bola de massa descreve uma circunferência num plano vertical presa a um fio de comprimento e massa desprezível (vide figura). A outra extreminade do fio (ponto da figura está presa a um dinamômetro (balança de mola) que registra a tensão no fio em cada instante. A tensão no fio é quando ele forma um ângulo de com a vertical.
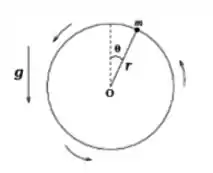
- Qual é a rapidez da bola quando ;
- Qual é o módulo da aceleração da bola quando .
Passo 1
No momento inicial, é necessário que se destaquem todas as forças atuantes no corpo a ser estudado. No caso, temos a força peso (para baixo) e a tração (na direção e sentido do fio).
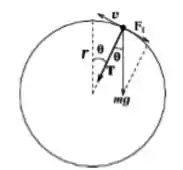
Passo 2
Como o problema pede a velocidade, a única forma de achar é através da aceleração centrípeta. Com isso, qual a melhor equação de força resultante a escolher?
Exatamente! Vamos começar pelo sentido radial do movimento:
Passo 3
Para achar o módulo da aceleração, precisamos de ambas as acelerações centrípeta e tangencial.
Tendo os valores de e , calculamos a :
Passo 4
Para a próxima aceleração, precisamos usar a equação da força tangencial resultante. Com isto, temos:
Passo 5
Por fim, calculamos o módulo da aceleração resultante da bola conforme a equação da soma vetorial que você já tem de cor: