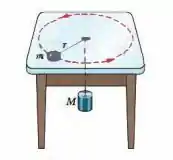
(Cap 6 – Ex 55) Um disco de metal de massa descreve uma circunferência de raio sobre uma mesa sem atrito enquanto permanece ligado a um cilindro de massa pendurado por um fio que passa por um furo no centro da mesa (Fig. 6-43). Que velocidade do disco mantém o cilindro em repouso?
Passo 1
Oláaaa, querido! Cê tá bem?
Então galera , nós sabemos que para que o disco permaneça em repouso, o módulo da tensão do fio deve ser igual ao peso do cilindro , uma vez que :
A massa do disco é
O raio do círculo
Convertendo cm para m, temos
A massa do cilindro é
A aceleração devido á gravidade é
Passo 2
Como a tensão do fio é a força centrífuga que mantém o disco em uma trajetória circular, . Assim, . Aplicando a segunda lei de Newton, isolando a velocidade na equação temos que :
Resposta
Tranquilo pessoal?? Bora resolver mais questões então