Um observador em repouso observa o movimento circular uniforme de um objeto sujeito a ação de apenas 2 forças. É correto afirmar que:
(a) Nenhuma das forças pode ter a direção tangencial.
(b) Uma das duas forças necessariamente aponta para o centro do círculo.
(c) As duas forças devem ser radiais e apontar para o centro do círculo.
(d) As duas forças devem ser radiais e pelo menos uma delas deve apontar para o centro do círculo.
(e) É possível que nenhuma das forças aponte para o centro do círculo.
Passo 1
O enunciado disse que um objeto realiza um Movimento Circular Uniforme.
Logo, já pensamos que há uma Força Centrípeta, certo?
Faz sentido, já que para haver um movimento circular, deve haver alguma força atuando como centrípeta, que aponta para o centro da trajetória circular (direção radial) e sempre está mudando a direção da velocidade, né?
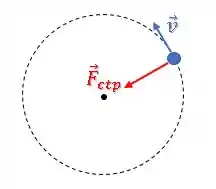
Mas existe um detalhe nessa história toda.
A Força resultante deve atuar como força centrípeta, porém, nada exige que ambas as forças estejam atuando apenas como centrípeta (na direção radial).
Então, poderíamos ter uma configuração como essa aqui:
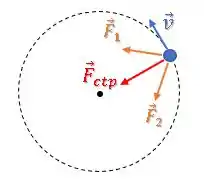
Onde a força resultante das forças e é uma força que atua radialmente (apontando para o centro), a famosa força centrípeta.
Assim, ficamos com a alternativa (e) e eliminamos (b), (c) e (d).
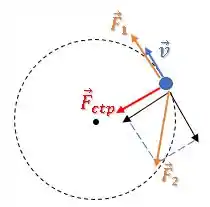
Já a alternativa (a), também está errada!
Isso porque poderia ser tangencial, desde que conseguisse cancelar a componente tangencial de e ainda resultar em uma componente radial que atua como força centrípeta, o que manteria o Movimento Circular Uniforme.
Resposta
Letra (e)