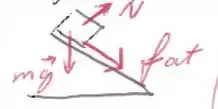
Um carro faz uma curva de raio numa pista plana (isto é, na figura) com atrito.
- Faça o diagrama das forças para o carro. Desconsidere a força de resistência do ar e as forças de atrito que retardam o movimento do carro.
- Encontre o coeficiente de atrito estático mínimo entre os pneus do carro e a pista, , para que o carro faça a curva com velocidade de módulo igual a .
- Considere agora que o carro faz uma curva de raio numa pista sem atrito e inclinada de um ângulo (vide figura). Faça o diagrama de forças e encontre o módulo da velocidade do carro, , neste caso.
- Se na situação do item o motorista aumentar o módulo da velocidade do carro para , o que acontece com o raio de curvatura da trajetória? Se houvesse atrito entre os pneus e a pista, para que lado apontaria a força de atrito neste caso? Repita o diagrama de forças incluindo a força de atrito.

Passo 1
a)
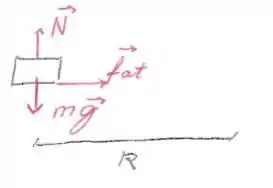
Desconsiderando a força de atrito que retarda o movimento do carro, ficamos apenas com a força de atrito produzida pela curva que o carro faz, apontando para o centro da curva.
Passo 2
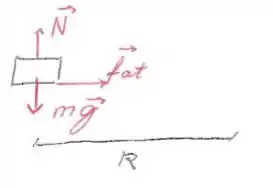
b)
A força resultante na horizontal é a força centrípeta. Logo:
Substituindo as fórmulas:
Como o carro não se move na vertical, . Substituindo:
Passo 3
c)
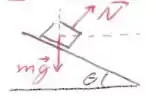
O diagrama de forças vai ser composto apenas pela força peso e normal.
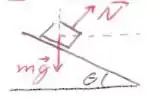
Decompondo a força normal nos eixos e , temos:
No eixo :
No eixo , temos a resultante centrípeta:
Substituindo a força normal:
Passo 4
d)
No item anterior nós descobrimos que:
Logo, se a velocidade for aumentada, consequentemente, o raio da curvatura terá que aumentar para manter a equação acima verdadeira.
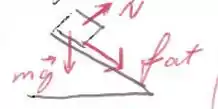
No caso de ter força de atrito, ela será como a do item . Ela contribuirá para a força centrípeta.
Resposta
a)
b)
c)
d) O raio da curvatura irá aumentar.