Um carro de corrida de massa igual a 500kg parte do repouso numa pista circular horizontal de raio igual a 400 m. Sua rapidez aumenta à taxa constante de 0.50 m/ .
(a) Explique e represente por meio de um desenho o que acontece com a direção do vetor aceleração à medida que a rapidez do carro vai crescendo.
(b) Quanto tempo levará até as magnitudes das acelerações radial e tangencial tornarem-se iguais?
(c) No instante do item (b), indique num desenho a direção e o sentido da força de atrito exercida pela estrada sobre o carro e determine sua a intensidade.
Passo 1
No item A, precisamos entender o que acontece com o vetor aceleração:
O enunciado nos diz que a rapidez do carro aumenta à taxa constante de , logo a componente tangencial da aceleração é constante:.
A componente radial da aceleração ou aceleração centrípeta aumenta à medida que a rapidez do carro vai crescendo, já que:
Assim, a aceleração é tangente à pista no instante inicial (t=0), já que o carro está em repouso e a velocidade é zero, não tendo, então aceleração centrípeta.
À medida que a aceleração centrípeta vai aumentando o vetor aceleração vai se inclinando cada vez mais, conforme mostra a figura abaixo:
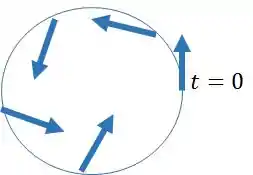
Passo 2
O item B pergunta em quanto tempo as acelerações centrípeta e tangencial serão iguais:
Nesse momento:
O instante que essa velocidade é alcançada pode ser determinado por:
Passo 3
No item c, iremos calcular a direção, o sentido e módulo da força de atrito nesse instante em que aceleração centrípeta e tangencial são iguais:
A força de atrito dos pneus com a pista é que mantém o carro em movimento circular com aceleração tangencial constante.
Pela segunda lei de Newton, a intensidade da força de atrito é:
Como o módulo da aceleração total é dado pela resultante da centrípeta com a tangencial:
O vetor força de atrito é paralelo ao vetor aceleração total.
Como as duas acelerações são iguais, ele fará um ângulo de 45° com a direção radial, conforme mostra a figura abaixo:
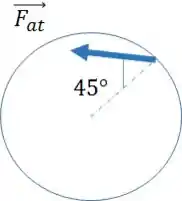
Resposta
-
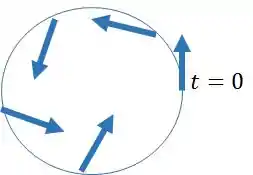
- e direção e sentido paralela à aceleração total fazendo 45° com a direção radial.