Um corpo de massa igual a está preso a um fio ideal. O corpo move-se ao longo de um círculo vertical de raio igual a sob a ação exclusiva da força gravitacional e da tensão no fio. O ponto A está localizado no topo do círculo, o ponto C está localizado no fundo do círculo. Os pontos B e D estão localizados exatamente a meio caminho entre os pontos A e C.
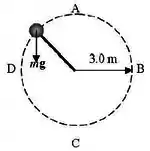
Qual das afirmativas abaixo é correta acerca da tensão no fio ?
(A) A tensão é menor no ponto A.
(B) A tensão é menor no ponto C.
(C) A tensão é menor nos pontos B e D.
(D) A tensão é a mesma nos pontos A e C.
(E) A tensão é a mesma em todos os pontos.
Passo 1
Como não há forças dissipativas atuando, podemos conservar a energia do sistema.
Considerando o ponto C como ponto zero do referencial, podemos dizer que no ponto C teremos apenas energia cinética. A energia potencial gravitacional aumenta nos pontos B e D e tem seu maior valor no ponto A. Com isso, a energia cinética é maior em C, diminui nos pontos B e D e tem seu menor valor em A. A energia cinética é dada por:
Logo, podemos dizer que:
Passo 2
Analisando a força centrípeta para cada um dos pontos, teremos:
Ponto A:
Como a velocidade em A é a menor e ainda descontamos o valor da força peso , podemos dizer que a tensão é menor no ponto A.
Pontos B e D:
Como as velocidades em B e D estão entre as velocidade de A e C e no cálculo de tração para estes pontos a força peso não é envolvida, podemos dizer que a tensão nestes pontos é maior que no ponto A e menor que no ponto C.
Pontos C:
Como a velocidade em C é a maior e ainda somamos o valor da força peso , podemos dizer que a tensão é maior no ponto C.
Logo,