Um carro realiza uma curva de raio em um plano inclinado sem atrito, de forma que o ângulo de inclinação do plano é suficiente para que o carro faça a curva sem subir ou descer no plano. Assinale a alternativa que corretamente relaciona o ângulo de inclinação com a velocidade do carro e o raio da curva:
a)
b)
c)
d)
e)
Passo 1
Esse tipo de questão, fica infitamente mais fácil quando a gente dá uma desenhada para entender o que está rolando. Primeiro, interpretando o enunciado, a gente percebe que tem um carro, realizando uma curva, e ele está em um plano inclinado. Ele consegue fazer essa curva, sem descer ou subir o plano.
Vamos desenhar isso:
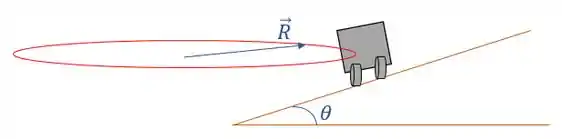
Passo 2
Agora que a gente já tem o desenho e entendeu a situation, vamos fazer o diagrama do corpo livre do nosso carrinho.
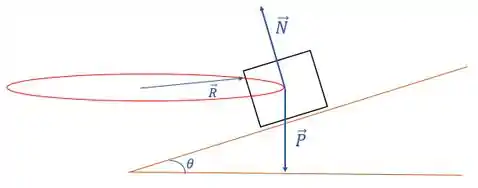
Podemos decompor essa força normal, em uma normal na direção do peso (eixo y) e uma normal na direção do raio da curva (eixo x).
Faremos isso, pois assim, podemos igualar a componente x da normal com a força centrípeta, e Tcharam, a questão está resolvida.
Em y:
Em x:
Resposta
Letra c)