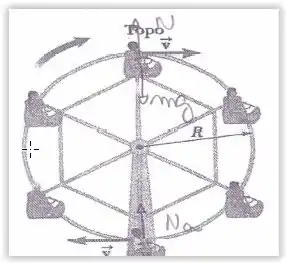
Uma criança de massa anda numa roda gigante como mostra a figura. A criança se move em um círculo vertical de raio com rapidez de
- Determine a força exercida pelo assent sobre a criança no ponto mais baixo da roda-gigante. Faça o diagram de corpo livre neste ponto.
- Determine a força exercida pelo assent sobre a criança no ponto mais alto da roda-gigante. Faça o diagram de corpo livre neste ponto.
- Suponha que um defeito no mecanismo da roda-gigante cause um aumento na velocidade da criança, que vai para . Qual é o peso da criança no topo da roda-gigante neste caso?
Passo 1
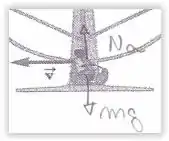
Como a roda está girando, devemos igualar a força resultante a força centripeta.
Substituindo os valores dado pelo enunciado temos:
Passo 2
A idéia aqui vai ser a mesma da letra anterior, a única diferença vai ser que vamos inverter o sinal das forças
Passo 3
Usando a mesma lógica que a letra anterior, vamos calcular a Normal pra saber quanto de peso é sentido pela criança
O peso sentido é praticamente zero, ou seja, ela está na iminência de sair pela tangente.
Resposta
Exercícios de Livros Relacionados
Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a 29k m / h faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é 0,32 ?
Em um brinquedo de parque de diversão, um carro se move em uma circunferência vertical na extremidade de urna haste rígida de massa desprezível. O peso do carro com os passageiros é 5,0k N e o raio da
Um estudante que pesa 667N está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal F N exercida pelo assento sobre o estudante é 556N . (a) O
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =107m , que a massa
Um bonde antigo dobra urna esquina fazendo uma curva plana com 9,1m de raio a 16k m / h . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?