UFF, Física 1, Prova 1, 2016.1
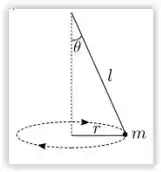
Considere o pêndulo cônico mostrado na figura. Neste pêndulo, uma particula de massa m presa à extremidade de um fio ideal de comprimento l gira com velocidade angular constante ω, descrevendo um círculo de raio r. O módulo da tensão T no fio é:
(A)
(B
(C)
(D)
(E
Passo 1
Essa é a típica questão de pêndulo cônico.
A sacada aqui está em decompor a tração em e , sendo e
Se liga na figura abaixo:
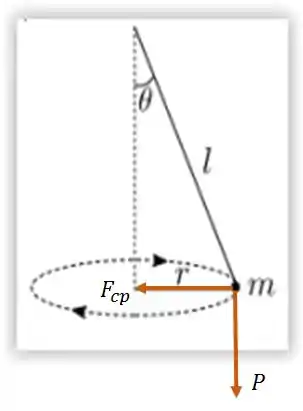
Show!
Como as informações dadas são o raio e a velocidade angular, vamos trabalhar com a força centrípeta.
Sabemos que e que
Substituindo por , montamos:
Passo 2
Já achamos o valor da força centrípeta e, por consequência, o valor de :
Agora precisamos relacionar com .
Pela figura vemos que
Mas nenhuma das respostas tá em função de . O que fazemos?
Se repararmos bem, o é dado no problema, pois .
Agora ficou fácil!
Podemos substituir:
Resposta
(B)