Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Centrípeta

Ver Teoria
Exercício 101234567891112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Homer, que possui massa M , decide se aventurar no Globo da morte. Para isso ele deseja calcular a velocidade que ele pretende ficar para conseguir fazer o movimento. Como ele é “limitado” ele precisa da sua ajuda. Considerando que ele manterá uma velocidade constante v , e o raio do Globo da morte é R , e que o atrito neste caso é desprezível. Considere também que o módulo da aceleração da gravidade é g . Determine

a) a força normal quando a moto passa na parte mais baixa do Globo.

b) a força normal quando a moto passa na parte mais alta do Globo.

c) a velocidade mínima para ele conseguir fazer a volta no Globo.

Passo 1

Os dados do problema são

D a d o s v R g

Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.

a)

Vamos responder as perguntas do passo a passo para colocar as forças

  1. A massa dele é considerada?

    2. Sim, ele tem massa.

  2. Ela esta encostada em alguma superfície?

    3. Sim, o bloco está em contato com o chão.

  3. Tem algum fio?

    4. Não, não existe um fio atuando.

  4. Tem mola?

    5. Não, não existe mola atuando.

  5. Tem atrito?

Não, não existe atrito.

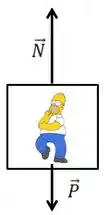
Teremos então o segundo DCL na parte mais baixa do globo

Passo 2

Nesse problema, ele está fazendo uma curva. Então devemos determinar a força resultante na direção do centro da curva, que será a força centrípeta

A força resultante na direção do centro da curva é

F r = F c p = N - P

m v 2 R = N - m g

N = m v 2 R + g

Passo 3

b)

Vamos começar respondendo a pergunta do passo a passo para montar o DCL.

  1. Sim, tem massa.
  2. Sim, ele está apoiado no chão.
  3. Não temos um fio.
  4. Não temos mola.
  5. O atrito é desprezível

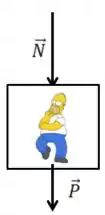
Teremos então o segundo DCL na parte mais alta do globo

Passo 4

Nesse problema, ele está fazendo uma curva. Então devemos determinar a força resultante na direção do centro da curva, que será a força centrípeta

A força resultante na direção do centro da curva é

F r = F c p = N + P

m v 2 R = N + m g

N = m v 2 R - g

Passo 5

c)

A velocidade mínima é aquela onde faz a Normal em um dado ponto ser zero. O ponto crítico no globo da morte é na parte mais alta do Globo da Morte, então

N = m v 2 R - g = 0

v 2 R = g

v = g R

Resposta

  1. N = m v 2 R + g
  2. N = m v 2 R - g
  3. v = g R

Exercícios de Livros Relacionados

Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a 29k m / h faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é 0,32 ?
Em um brinquedo de parque de diversão, um carro se move em uma circunferência vertical na extremidade de urna haste rígida de massa desprezível. O peso do carro com os passageiros é 5,0k N e o raio da
Um estudante que pesa 667N está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal F N exercida pelo assento sobre o estudante é 556N . (a) O
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =107m , que a massa
Um bonde antigo dobra urna esquina fazendo uma curva plana com 9,1m de raio a 16k m / h . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?