Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
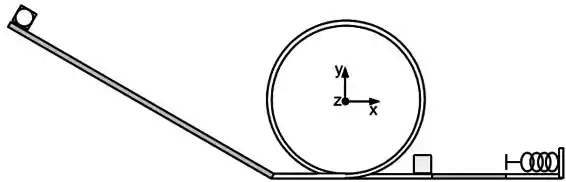
d) Um mecanismo segura o disco na base do plano e somente o cubo prossegue para fazer o percurso do trilho. Determine a aceleração total do cubo quando seu centro de massa está na posição . Suponha que na base do trilho a velocidade do cubo é de .
Passo 1
d)
Na posição solicitada temos duas acelerações atuando. A aceleração centrípeta apontando na direção de e a aceleração da gravidade apontando na direção de :
Lembrando que , onde é a distância do centro de massa do cubo até o centro da trajetória:
Como não tem atrito nesse trecho do percurso, podemos aplicar a conservação de energia:
Substituindo na equação:
Resposta
d)