Suponha que o coeficiente de atrito estático entre os pneus de um carro de massa e a estrada onde ele trafega é
- Considerando que a pista é completamente plana, qual é a maior velocidade escalar com a qual o carro pode fazer uma curva de raio R sem derrapar (deslizar)?
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Uma pista plana significa que o carro não faz ângulo nenhum com o chão, então a normal é balanceada pela força peso. Beleza?
E se esse carro está fazendo uma curva, na horizontal a resultante das forças é a força centrípeta! A força de atrito é contrária ao movimento, então se a curva é para direita, a força de atrito aponta para a esquerda, que nem nesse esquema aqui:
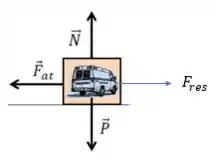
A ideia aqui é equacionar as forças tanto na vertical, quanto na horizontal e determinar a velocidade que deixa tudo equilibrado =)
 mas calma, vou fazer junto com você!
mas calma, vou fazer junto com você!
Passo 2
Na vertical, como comentei ali no passo anterior, a normal é balanceada pelo peso:
Assim temos a primeira equação
E na horizontal, temos apenas a força de atrito, que deve ser igual à força centrípeta, pois é a força resultante agindo no carro na direção :
 E qual será essa força resultante? É a força centrípeta! Lembra que o carro está descrevendo uma curva! Então temos a segunda equação (e que envolve a variável que queremos, a velocidade)
E qual será essa força resultante? É a força centrípeta! Lembra que o carro está descrevendo uma curva! Então temos a segunda equação (e que envolve a variável que queremos, a velocidade)
Agora nosso trabalho é juntar essas duas equações para eliminar a força N, pois ela é desconhecida, e isolar em termos das quantidades conhecidas: e
Passo 3
Da primeira equação
E substituindo na segunda:
Podemos simplificar a massa dos dois lados:
Essa é a velocidade que o carro precisa ter para não derrapar!
E é isso!
Espero ter ajudado!