4) Rendimento de uma máquina térmica.
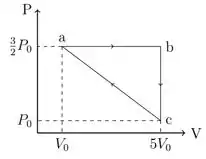
Uma certa quantidade de gás ideal é submetida ao ciclo indicado no diagrama da figura. O calor rejeitado na etapa vale . O calor transferido na etapa vale:
1.
2.
3.
4.
5.
6.
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, essa questão deu pra gente um diagrama e disse que na etapa temos uma quantidade de calor rejeitado que vale . O que devemos descobrir é a quantidade de calor que está sendo transferida na etapa . Então vamos dar uma olhada melhor no que está acontecendo nessa etapa.
Perceba que a transformação que está etapa é uma transformação isobárica, pois a pressão está fixa em . Assim, ela pode ser escrita como:
Mas perceba que não temos todas essas informações, então vem comigo que vamos descobrir cada uma delas jutos.
Passo 2
Vamos começar lembrando da equação dos gases ideais que diz que
Assim podemos escrever e , como:
E
Assim, nossa equação para o calor se torna:
Podemos colocar em evidência. E no gráfico a gente consegue essas informações de Pressão e Volume para os pontos e . E substituindo teremos:
Arrumando um pouco melhor, ficaremos com:
Que melhorando ainda mais, se torna:
Maravilha!
Passo 3
Mas não sabemos ainda quem é , então vamos usar a informação que o problema nos deu de que na etapa temos uma quantidade de calor rejeitado que vale .
Como na etapa de , de acordo com o gráfico, a transformação que está acontecendo é isovolumétrica, podemos lembrar que:
Se descobrirmos , podemos encontrar e volta para o cálculo de . Então esse é o plano.
Sendo:
Podemos colocar em evidência. E no gráfico a gente consegue essas informações de Pressão e Volume para os pontos e . E substituindo teremos:
Arrumando um pouco melhor, ficaremos com:
Como o problema nos disse que nessa etapa o calor está sendo rejeitado, teremos um calor negativo, já que ele está saindo do sistema. Assim:
E igualando teremos:
Isolando , ficamos com:
Maravilha, agora vamos voltar para , que é:
Substituindo teremos:
Agora, basta calcular o calor pedido.
Passo 4
No final do passo 2, vimos que:
Substituindo ficamos com:
O que resulta em:
E finalmente, encontramos a alternativa correta que é a número 1.
Prontinho!!
Resposta
Resposta:
1.