A figura mostra duas curvas adiabáticas em um diagrama PV de um gás ideal.
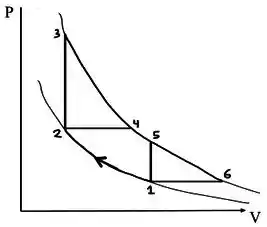
É possível construir diferentes máquinas térmicas que envolvam compressões e expansões adiabáticas do gás ao longo dessas mesmas duas curvas. Por exemplo, o mesmo trecho de compressão adiabática pode ser incluído em um chamado ciclo de Brayton (composto de dois trechos adiabáticos e dois trechos isobáricos) e num chamado ciclo de Otto (composto de dois trechos adibáticos e dois isovolumétricos). Os rendimentos destes ciclos são dados respectivamente pelas expressões:
Onde e são as razões entre a máxima e mínima pressão (resp. , volume) atingidos ao longo de cada ciclo respectivo.
Comparando as eficiências dos ciclos de Brayton e de Otto contendo o trecho 1-2 na figura acima, podemos concluir que
A)
B)
C)
D) pode ser , ou que , dependendo do valor da pressão no ponto 1
E) pode ser ou que , dependendo do valor de
Passo 1
Vamos tentar achar esses ciclos no gráfico.
Ciclo de Brayton: dois trechos adiabáticos e dois isobáricos, logo é o ciclo (1246).
Ciclo de Otto: dois trechos adiabáticos e dois isovolumétricos, logo é o ciclo (1235).
Passo 2
No ciclo de Brayton (1246), precisamos calcular ,
Que, no caso, ocorre entre as pressões e . Então,
No ciclo de Otto (1235), precisamos calcular ,
Este ciclo ocorre entre os volumes e . Então,
Passo 3
Mas como relacionar as pressões e os volumes 1 e 2?
Podemos usar o fato que o processo é adiabático, então podemos dizer que
Ou seja,
Passo 4
Vamos substituir isso em algum dos rendimentos. Eu escolhi substituir no Brayton:
Que é exatamente o valor para o !!
Resposta
B)