UFPE, Física 2, 3º EE - 2018.1, Questão p1
substância de trabalho de uma máquina térmica opera no ciclo mostrado no diagrama pressão-volume abaixo. Considere que a substancia de trabalho se comporta como um gás ideal monoatômico.
- (1,0) Calcule, em termos de p0 e , o trabalho realizado pela substância em cada um dos processos .
- (1,5) Determine, em termos de , a energia transferida para a substância sob forma de calor em cada um dos processos .
- (1,0) Calcule a eficiência " da máquina térmica operando no ciclo .
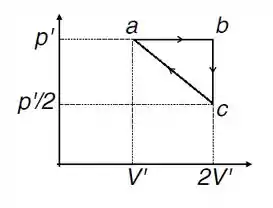
Passo 1
a) O trabalho em cada processo é dado pela área abaixo da curva correspondente no diagrama . Assim, é podemos calcular o trabalho como:
Se observarmos a área abaixo da curva ca, parece que temos um triângulo em cima de um retângulo, então para calcularmos essa área usamos ambas as fórmulas, primeiro calculamos a parte retangular:
Agora a triangular:
Somamos tudo:
Mas se a gente observar de c até a estamos “voltando”, então o trabalho será negativo:
Passo 2
b) O processo ocorre sob pressão constante. Então temos que:
.
Como , com a pressão mantida constante temos . Assim:
O processo se dá a volume constante. Então:
Como , com o volume mantido constante temos . Assim:
Como no ciclo a energia interna não varia, podemos afirmar que:
Substituindo os resultados anteriores chegamos a:
Passo 3
c) O rendimento de uma máquina térmica é definido por:
onde o é o trabalho útil obtido no ciclo e é o calor absorvido pela substância de trabalho no ciclo. Das respostas em (a) temos que:
Além disso, só há um processo em que a substância absorve calor, que e a expansão a pressão constante , portanto:
A eficiência é, portanto:
Resposta
a)
b)
c)