Uma máquia térmica opera com um gás ideal segundo o ciclo representado no diagrama PV ao lado. Qual das afirmações abaixo é correta?
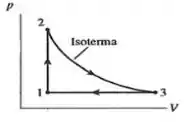
- O gás recebe calor no estágio 1 2 e cede calor nos estágios 2 3 e 3 1.
- O gás recebe calor nos estágios 1 2 e 2 3 e cede calor no estágio 3 1.
- O gás recebe calor no estágio 1 2, cede calor no estágio 3 1 e não há troca de calor no estágio 2 3
- O gás recebe calor no estágio 2 3 e cede calor nos estágios 1 2 e 3 1
- O gás cede calor no estágio 1 2 e recebe calor nos estágios 2 3 e 3 1
Passo 1
E aí, galerinha! Tudo na paz por aí?
Sabe qual é o primeiro bizu que eu vou te dar nesse problema aqui e que não foi dito no enunciado de propósito? Em termodinâmica, três variáveis são super interligadas. Você sabe quais são? Elas são pressão, volume e temperatura. Note que esse gráfico aí deu pra gente a variação de pressão com o volume, certo?
Opa, então tá faltando uma daquelas variáveis que eu te disse antes, e, qual é? Temperatura.
Quando isso acontecer, essa variável que está faltando é a variável que ficou CONSTANTE durante todo esse processo de variação no gráfico.
Em outras palavras, para uma curva em um gráfico PV de um gás ideal, a temperatura foi mantida constante, ou seja, um processo ISOTÉRMICO!!!
Tá, mas e onde tá a quantidade de calor absorvida nesse rolê todo aí? Bem, qual é a equação na termodinâmica que consegue nos dá a quantidade de calor?
Onde são a variação da energia interna, quantida de calor e trabalho, respectivamente.
Agora que já vimos a equação que vai nos dar a variável de interesse, precisamos ver como obter o valor de e .
VEM COMIGOOOOOOOOO!!!
Passo 2
Para um gás ideal, é observado que a energia interna é dependente unicamente da temperatura.
Se aplicarmos a diferenciação nessa equação teremos:
Integrando, temos:
Como nosso processo é isotérmico, teremos que !! E nossa, esse é exatamente nosso caso, afinal, estamos falando de um processo ISOTÉRMICO!!
Passo 3
Beleza, agora que vimos e o enunciado dá pra gente vários opções sobre o “calor” que o gás recebe, o que ele tá perguntando é:
E você se lembra como se calcula o trabalho de expansão/contração ?
Passo 4
Vamos agora analisar as etapas: .
: Pressão aumenta com volume constante: Se volume é constante, trabalho é zero, e portanto, para que isso aconteca é necessário CEDER calor ao gás.
: A temperatura se mantém constante enquanto o volume varia: Para isso acontecer, um reservatório térmico tem que ceder calor ao gás para que a temperatura não variar.
Volume está diminuindo e a pressão permanece constante: Para isso acontecer é preciso que a temperatura do gás seja reduzida, ou seja, o gás precisa dar calor ao ambiente.
Olhando pras nossas alternativas, qual é a opção que bate com os comportamentos físicos acima?
Passo 5
Olhando para as nossas alternativas, observamos que a letra (B) tem exatamente o comportamente físico que explicitamos acima.
E assim, fechamos mais uma questãooooo, galeraa
Resposta
(B)