Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 20 – Problemas – 46.
(Cap 20 – Prob 46) Calcule a eficiência térmica da máquina que usa moles de um gas ideal diatômico e executa o ciclo mostrado na Figura 20.27.
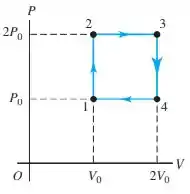
Passo 1
Falaai galerinha, show de bola?
Bora resolver essa comigo?
A gente pode ver pelo ciclo, que tem dois processos isobáricos e dois isocóricos. Nos processos isocóricos o gás não realiza trabalho e o trabalho total do ciclo só envolve os outros dois processos:
E os únicos processos em que ocorre absorção de calor são e , porque em um deles a pressão aumenta e no outro, o volume que aumenta. Então:
Nos outros dois, eles diminuem, e nesses casos o ciclo perde calor, mas não precisamos deles para calcular a eficiência, já que a equação de eficiência é:
Passo 2
Vamos começar calculando os trabalhos, os processos são isobáricos, então o trabalho é dado por:
Para o processo :
E para o :
O trabalho total fica:
Passo 3
Para os calores dos processos que vamos usar para calcular o calor absorvido, vamos precisar das equações que envolvem a variação de temperatura, só que o processo , está a volume constante, então:
E o processo está a pressão constante, assim:
Como a gente não tem a temperatura de cada processo, vamos usar a equação dos gases ideais para substituir a variação da temperatura em cada caso. Vamos primeiro fazer do processo :
Como podemos ver, o volume é constante, e a diferença entre os dois processos dá:
Isolando e substituindo os valores dados pelo gráfico:
Colocando na equação do calor:
Fazemos o mesmo para o processo , só que agora a pressão que é constante, então fica:
Substituindo na equação do calor:
E como foi dito antes, o calor total absorvido vai ser a soma dos calores desses dois processos:
Como :
Passo 4
Agora que temos tudo que precisamos, a gente coloca tudo na equação de eficiência:
Que fica:
Para um gás ideal diatômico:
A eficiência fica:
Passando para :