A figura mostra o ciclo de uma máquina térmica que usa gás com . A temperatura inicial é , e a máquina opera a ciclos por segundo.
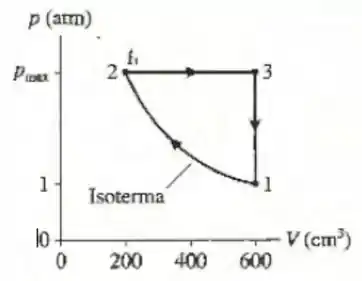
Qual é a potência de saída da máquina?
Qual é o rendimento térmico da máquina?
Passo 1
Para determinar a potência de saída da máquina, precisamos determinar o trabalho . Para determinar o trabalho, precisamos determinar e para cada um dos processos.
Para começar, precisamos determinar o número de mols do gás que temos, para isso, basta usar a clássica no ponto , pois conhecemos todos os dados para esse ponto, se liga:
Lembre-se de usar o !
agora que sabemos quantos mols estão envolvidos, podemos analisar cada processo do ciclo, começando pelo processo isotérmico:
Processo (isotérmico)
Processo (isobárico):
A gora que temos todas as informações do ciclo, podemos determinar e em cada processo, se liga no próximo passo!
Passo 2
Para o processo , temos:
Substituindo os valores, temos:
No processo isotérmico, temos:
Para o processo , temos:
Substituindo os valores, temos:
No processo isobárico, temos:
Pausa para calcular :
Então:
Voltando ao cálculo de , temos:
Para o processo , temos:
No processo isovolumétrico, temos:
Como já sabemos o valor de , , substituindo os valores, temos:
Agora que temos e para todos os processos, podemos determinar , basta somar!
Como temos que a máquina opera a ciclos por segundo, temos que a potência é dada por:
Passo 3
Para uma máquina térmica, temos que o rendimento é dado por:
Pelos cálculos, vemos que , substituindo, temos:
Resposta