Uma amostra com moles de um gás ideal cujo calor específico molar a volume constante vale realiza o ciclo ilustrado no diagrama abaixo.
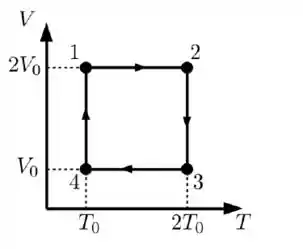
a) Faça um esboço do ciclo acima em um diagrama , indicando os estados , bem como a pressão e o volume de cada estado em função de e .
b) Determine o calor envolvido em cada etapa do ciclo.
c) Determine o trabalho total realizado no ciclo.
d) Este ciclo representa uma máquina térmica ou refrigerador?
Justifique a sua resposta.
Passo 1
a)
Vamos lá. Para fazer u diagrama temos que saber as pressões correspondentes de cada ponto. Então vamos aproveitar que é um gás ideal e , portanto, podemos usar a relação:
Do ponto 1 para o ponto 2:
Então
Mas, podemos melhorar isso. Para o ponto 2, vamos escrever:
Com isso, a pressão no ponto 1 fica:
Show!
Agora, a mesma coisa do ponto 2 para o ponto 3:
Substituindo:
Arrumando:
Ou seja,
Do 3 para o 4:
Substituindo:
Ou seja,
Resumindo: do 1 para o 2 temos que a pressão aumenta, a volume constante. Do 2 para o 3 o volume diminui a temperatura constante, do 3 para o 4 a pressão diminui a volume constante. Do 4 para o 1 o volume aumenta a temperatura constante.
Então, chamando de , o diagrama , fica:
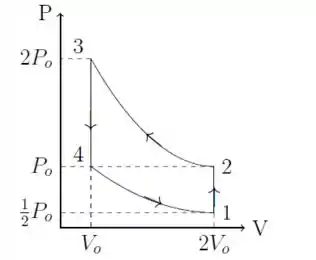
Passo 2
b)
Agora ele quer o calor para cada etapa. Vamos lá!
De 1 para 2: O volume é constante, então o trabalho é nulo. Pois
Pela primeira lei, sabemos que
Então nesse caso:
E como é um gás ideal a seguinte relação é válida:
Então
Substituindo:
De 2 para 3: Nessa etapa a temperatura fica constante. Então
Logo, pela primeira lei:
E o trabalho vale:
Usando a equação dos gases ideias temos
Substituindo:
Pelas propriedades do log:
Então
De 3 para 4, o volume permanece constante, então o trabalho é nulo. Logo:
E como
Temos
Substituindo:
Show!
De 4 para 1: Não há variação de temperatura, então .
Logo, pela primeira lei:
E o trabalho vale:
Portanto
Maravilha!!
Passo 3
c)
Como já vimos na letra B, quando o volume permanece constante o trabalho é nulo, logo E .
Os trabalhos e já foram calculados no item b).
E valem:
Assim, o trabalho total
Passo 4
d)
Como o trabalho total é negativo, temos que o ciclo representa um refrigerador. Pois ele precisa que uma energia seja fornecida a ele. O trabalho é realizado sobre o gás, ao contrário da máquina, que é o gás que produz trabalho.
Resposta
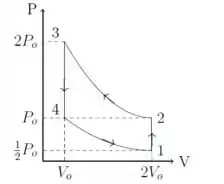 a)
a)
b)
De 1 para 2:
De 2 para 3:
De 3 para 4:
De 4 para 1:
c)
d)
Como o trabalho total é negativo, temos que o ciclo representa um refrigerador. Pois ele precisa que uma energia seja fornecida a ele. O trabalho é realizado sobre o gás, ao contrário da máquina, que é o gás que produz trabalho.