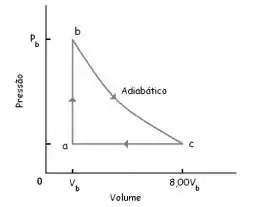
A figura mostra um ciclo reversível percorrido por de um gás monoatômico ideal. O processo é uma expansão adiabática, com e. Para este ciclo, encontre:
A energia adicionada ao gás na forma de calor.
A energia liberada pelo gás na forma de calor.
O trabalho líquido realizado pelo gás
A eficiência do ciclo
Dados:
- gás monoatômico: , e
- pressão atmosférica
Passo 1
Bom galera, vamos utilizar uma série de relações importantes envolvendo gases pra resolver essa questão. Então apertem os cintos, lá vamos nós:
Bem, queremos saber aqui qual a quantidade de calor que adicionada ao ciclo pra que esse realize trabalho. Poderíamos analisar transformação por transformação e achar a contribuição de cada uma para o calor fornecido. Mas, vamos pensar um pouco sobre esse ciclo:
No trecho
Não há troca de calor aqui, pois é uma transformação adiabática (. O calor que foi fornecido ao ciclo não pode ter sido “injetado” aqui, né? (:
No trecho :
Bem, aqui há troca de calor. Porém, como o trabalho é negativo (o gás está se contraindo, diminuindo o seu volume), é de se esperar que esse seja o ponto de rejeição de calor para a fonte fria!
No trecho :
É aqui onde o calor tem que ser fornecido! Agora, precisamos calculá-lo:
Usando a primeira lei:
Perceba, pelo gráfico, que não há variação de volume nesse trecho! É uma transformação isovolumétrica, e isso quer dizer que . Logo:
Ok! Então basta calcularmos a variação de energia interna pra acharmos o trabalho. Lembrando que:
Temos o valor de e , mas precisamos descobrir o valor de .Vamos usar a equação geral dos gases para isso:
Vamos achar primeiro a temperatura do ponto , pois já temos o valor da pressão e volume desse ponto:
Agora vamos calcular . Pra isso, precisamos da pressão e do volume desse ponto, porém só temos o valor do volume. Mas perceba que a pressão daquele ponto é a mesma que a pressão do ponto !
Vamos descobrir então a pressão do ponto c. Como há uma transformação adiabática entre e , podemos achar a pressão de através da equação das transformações adiabáticas:
Como :
Então, vale:
Substituindo esse valor e os outros do enunciado na expressão que encontramos pro calor:
Conseguimos! Galera, não se assustem, esse tipo de questão é como um quebra cabeça. Aos poucos vamos descobrindo as informações de cada ponto do ciclo, e elas podem ser usadas nas outras opções da questão.
Passo 2
Agora queremos saber qual foi o calor rejeitado. Lembra da nossa análise? Vimos que o processo em que ocorrerá a liberação de calor para a fonte fria é o processo ! Vamos analisar esse processo com a primeira lei:
Podemos calcular :
Agora precisamos descobrir o valor de . Bom, uma forma de se descobrir isso é se lembrando que a variação total da energia interna em um ciclo é 0. Isso também nos diz que a soma das variações de cada trecho tem que ser igual a 0:
No trecho sabemos que :
Podemos calcular a variação e energia interna no trecho
Já foi calculado e vale:
A gente pode calcular facilmente, pois já temos a pressão e o volume do ponto c:
Logo:
Agora vamos descobrir :
Agora, sabendo o valor do trabalho e da variação de energia interna:
Passo 3
Essa é fácil! Depois de todo aquele trabalho, temos todas as informações pra resolver esse item! Vamos apenas usar a relação:
Outra que vamos resolver rapidamente já que já temos todas as informações necessárias. A eficiência de uma máquina térmica é:
Como:
Substituindo na expressão: