Uma amostra de um gás ideal () passa pelo processo mostrado na figura abaixo.
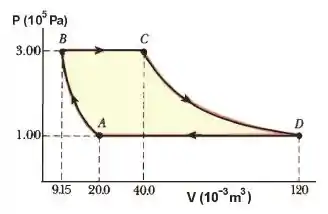
De a , o processo é adiabático. De a é isobárico com de energia entrando no sistema por calor. De a , o processo é isotérmico. De a , é isobárico com de energia saindo do sistema por calor.
- Encontre as temperaturas dos estados , e do processo isotérmico.
- Responda, justificando, se o gás é mono-, di- ou poliatômico.
- Reproduza a tabela abaixo no caderno de respostas. Complete-a, justificando, com os valores de , e para cada um dos processos e para o ciclo.
- Calcule a eficiência de uma máquina que funcione com esse ciclo.

Passo 1
Vamos usar a equação geral dos gases pra calcular os valores das temperaturas:
A:
B:
C:
Vamos usar a expressão:
Nos pontos e
Como o processo é isotérmico, é igual à :
Passo 2
b):
Vamos usar a transformação adiabática pra resolver isso:
Porque a partir do valor de nós descobrimos de que tipo é o gás. Aplicando dos dois lados:
Sendo e :
Logo o gás é diatômico. Por que para um gás diatômico temos;
Passo 3
c):
Vamos primeiro calcular cada quantidade termodinâmica separadamente e depois preencher a tabela.
Primeiro o calor:
No processo
Como é um processo adiabático, por definição:
:
Nesse ponto vamos usar a equação do calor:
Sendo o calor específico molar à pressão constante. Bem, a gente sabe as temperaturas de todo mundo né?
Então vamos lá. Fazendo :
Nesse caso, temos uma transformação isotérmica. Como é uma transformação desse tipo,
Pela primeira lei:
Fazendo :
Logo:
Vamos fazer como no processo
E por fim, o calor do ciclo será a soma disso tudo:
Passo 4
Trabalho:
Pela primeira lei, como
Sendo
Logo:
Aqui é fácil. A pressão é constante, então o trabalho será:
:
Como vimos:
Esse valor de trabalho também é fácil de calcular por se tratar de uma transformação isobárica:
E o trabalho do ciclo vai ser a soma de todo mundo:
Passo 5
Variação da energia interna:
Por se tratar de uma transformação adiabática:
Vamos aplicar aqui a primeira lei:
Por ser uma transformação isotérmica:
Isso acontece pois a energia interna é uma função da temperatura, e vice-versa.
Vamos aplicar aqui a primeira lei novamente:
Então, a variação total de energia interna do ciclo será a soma de todas essas variações:
Como era de se esperar (:.
Vamos montar nossa tabelinha então:

Passo 6
d):
A eficiência de uma máquina térmica é dada por:
O calor quente é o calor que o gás recebe da fonte quente. Quando o gás recebe calor da fonte quente, ou ele se expande ou se aquece, ou acontecem as duas coisas.
Se analisarmos bem o gráfico, vamos perceber que isso ocorre nos processos e .
Então;
E o trabalho do ciclo vale:
Logo:
Resposta
a):
B:
C:
b):
o gás é diatômico
c):

d):