Um mol de um gás monoatômico ideal é utilizado como substância de trabalho de uma máquina térmica que opera de acordo com o ciclo mostrado no diagrama da figura. Suponha que e . A etapa corresponde a um processo irreversível em que o trabalho realizado vale

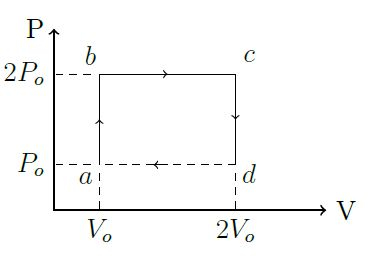
(a) Determine as temperaturas nos pontos , , e

(b) Determine o calor , o trabalho e a variação de energia interna em cada etapa deste ciclo

(c) Calcule a eficiência desta máquina térmica

(d) Determine a variação de entropia em cada etapa deste ciclo.

(b)

Vamos acertar a nossa estratégia aqui! Como já calculamos as temperaturas no passo anterior fica mais fácil relacionar a variação de energia interna com a variação de temperatura por

(Lembrando que )

Já o trabalho é dado por

Só que no nosso diagrama só temos processos isobáricos (pressão constante) e processos isovolumétricos (volume constante). Assim essa integral do trabalho fica fácil!

Agora pra achar o calor basta usar a primeira lei da Termodinâmica, já que já temos o calor e o trabalho de cada caso!

Belezinha? Vamos aplicar isso então!

Processo

Variação de energia interna

Trabalho

Calor

Processo

Variação de energia interna

Trabalho

Calor

Processo

Variação de energia interna

Trabalho

Calor

Processo

Variação de energia interna

Trabalho

Calor

(c)

Para calcular a eficiência dessa máquina podemos fazer

Onde é a soma dos calores recebidos pelo gás

E é a soma dos calores doados pelo gás

Assim

(d)

Pra calcular a variação de entropia, vamos usar

O processo é um processo isovolumétrico, então o calor infinitesimal é dado por

(Lembrando que )

Assim

Agora temos que lembrar que pra um gás monoatômico

Substituindo e os valores de temperatura que encontramos no passo 1:

O processo é um processo isobárico, então o calor infinitesimal é dado por

Assim

Agora temos que lembrar que pra um gás monoatômico

Substituindo e os valores de temperatura que encontramos no passo 1:

O processo é um processo isovolumétrico, então o calor infinitesimal é dado por

Assim

Já vimos que pra um gás monoatômico

Substituindo e os valores de temperatura que encontramos no passo 1:

Agora o processo é um processo irreversível!!! Não podemos usar diretamente! Mas a nossa salvação é que num ciclo a variação de entropia tem que ser nula! Assim

Outra forma de fazer, é o seguinte: o enunciado diz que o processo é irreversível. Como a entropia é uma função de estado, podemos pensar num processo reversível que tenha como estados inicial e final e e dizer que

O processo mais fácil de pensar é um processo isobárico conectando e . Nesse processo

Logo pro processo irreversível vai ser a mesma coisa

Mas cuidado! Você tem que deixar bem claro o raciocínio na hora de explicar que está usando um processo reversível para calcular um processo irreversível já que a entropia é uma função de estado, hein!!!