Três mols de um gás ideal monoatômico passam pelo ciclo termodinâmico descrito na figura( isobárico, isotérmico e isocórico):
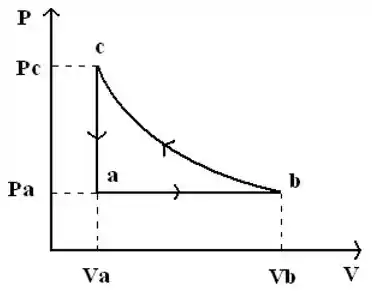
Dados , e , determine , e (tome e trabalhe com dois algarismos significativos).
Determine o trabalho realizado pelo sistema , o calor cedido ao sistema e a variação da energia interna para cada processo e preencha a tabela (justifique cada valor encontrado):

O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique
Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador), do ciclo.
Faça um gráfico do ciclo considerado.
Passo 1
Vamos primeiro reunir os dados fornecidos:
Analisando a figura, podemos dizer que:
Visto isso, podemos agora calcular o que foi pedido, vamos começar por
Passo 2
Para determinar , iremos utilizar a lei dos gases ideais:
Substituindo os valores que já temos:
Passo 3
Vamos agora determinar , para isso, iremos utilizar também a lei dos gases ideais:
Passo 4
Para determinar , usaremos, novamente a lei dos gases ideais:
Lembre-se que devemos utilizar apenas dois algarismos significativos!
Passo 5
Vamos analisar cada processo de uma vez, começando com :
Como temos um processo a pressão constante, podemos determinar o trabalho assim:
Para o calor trocado, sendo o processo a pressão constante, temos:
Para determinar a energia interna, podemos recorrer a primeira lei da termodinâmica:
Passo 6
Agora vamos analisar o processo :
Por ser um processo isotérmico, temos que a energia interna é zero!
Agora podemos calcular o trabalho realizado no processo:
substituindo por , temos:
Vamos agora substituir os valores conhecidos:
Pela primeira lei da termodinâmica, temos:
Passo 7
Finalmente, vamos analisar o processo :
Por ser um processo isovolumétrico, sabemos que o trabalho realizado é zero!
Vamos agora determinar o calor trocado no processo, que se dá a volume constante:
Pela primeira lei da termodinâmica, temos:
Agora é só completar a tabela!

Passo 8
Tendo em vista que o trabalho é negativo, e que o calor flui da fonte fria para a fonte quente, chegamos a conclusão de que se trata de um refrigerador.
Passo 9
Sabendo que se trata de um refrigerador, podemos calcular o coeficiente de desempenho:
Vamos primeiro calcular o trabalho realizado no ciclo:
Substituindo, temos:
Lembre-se que o calor retirado da fonte fria é :
Passo 10
Utilizando os dados obtidos no item , podemos montar o seguinte gráfico:
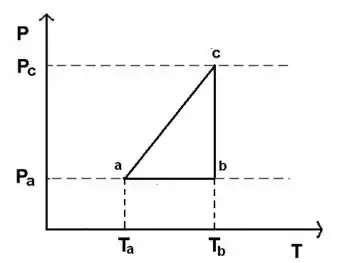
Resposta
; ;

Tendo em vista que o trabalho é negativo, e que o calor flui da fonte fria para a fonte quente, chegamos a conclusão de que se trata de um refrigerador.
