O funcionamento do motor a gasolina de seu carro pode ser tratado pelo modelo do Ciclo de Otto representado na figura abaixo. Neste motor, é o fator de compressão:

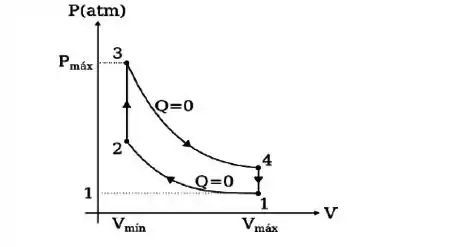
Usando as relações adiabáticas entre e , pode-se mostrar que o rendimento vale:

Bom, segundo a primeira lei da termodinâmica, o trabalho de uma transformação adiabática pode ser calculado por:

Como:

Como pode ser calculado por:

Então:

Bom, vamos tentar alterar um pouco o formato da equação que achamos:

Temos:

Vamos usar as equações:

Pra modifica-la:

Substituindo na equação inicial:

Beleza, já achamos uma equação que representa o trabalho de uma transformação adiabática. Bora calcular o trabalho total do sistema agora: Só há realização de trabalho nos trechos e . Os outros trechos ocorrem a volume constante.

Assim:

E:

O trabalho total será dado pela soma dos trabalhos:

Já temos o trabalho. Agora precisamos de duas coisas: Do calor fornecido ao ciclo e das relações adiabáticas envolvendo as temperaturas citadas no enunciado.

Em qual trecho o calor é fornecido?

Como nos trechos adiabáticos não há transferência de calor, só nos resta os trechos e . Quando um gás recebe calor, ele tende a inflar, ou seja, aumentar o seu volume, certo? Então o trecho onde o calor é fornecido ao gás é o trecho .

Esse calor pode ser calculado por:

Como vimos:

Assim:

E as relações adiabáticas envolvendo temperaturas?

Bom, pra isso é só você seguir por esse caminho aqui:

Usando a equação geral dos gases:

Assim:

Calma! Vamos que tá quase lá.

Voltando a equação do rendimento:

Substituindo os valores encontrados pro trabalho e pro calor fornecido:

Agora é a hora de a gente usar aas relações adiabáticas entre e :

Vamos escrever as temperaturas do denominador em função das temperaturas de baixo. Isso é:

E:

Agora vem o pulo do gato: vamos escrever com os chamados volumes máximos e mínimos que o enunciado exige. Olhando no gráfico, você pode perceber que os volumes: são os volumes máximos, assim como os volumes: são os volumes mínimos. Então podemos reescrever as relações acima como:

Lembrando que:

E:

Assim:

Fim!