Um mol de gás ideal monoatômico é submetido ao ciclo mostrado na figura.
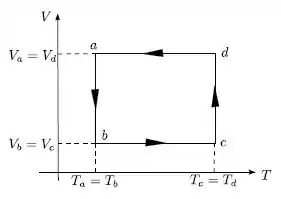
Desenhe o ciclo correspondente no plano (P.V) especificando o tipo de cada etapa.
Calcule o trabalho realizado (ou sofrido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Calcule o calor absorvido (ou cedido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Este ciclo corresponde a um motor ou a um refrigerador? Por quê?
Passo 1
Bom galera, pra desenhar isso ai é só você perceber qual é o processo que acontece em cada trecho:
: Processo isotérmico..
Processo isovolumétrico.
: Processo isotérmico..
Processo isovolumétrico. .
Então, o desenho ficará assim:
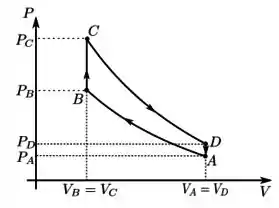
Passo 2
São 4 processos, mas dois deles acontecem a volume constantes. Então, o trabalho desses dois será igual à zero. Os outros dois processos são isotérmicos. Vamos lá:
: Processo isotérmico..:
O trabalho é dado por:
Como:
Então:
Show? Agora vamos substituir os valores que vemos no gráfico:
Como
É isso.
Processo isovolumétrico.
Como a gente viu:
: Processo isotérmico..:
Jogo rápido: Bem parecido com
Como
Processo isovolumétrico. .:
Como a gente viu:
Passo 3
Vamos lá:
: Processo isotérmico..:
Bom, como o processo é isotérmico, a variação da energia interna é nula e, pela primeira lei da termo, teremos:
Processo isovolumétrico.
O calor trocado aqui é o calor trocado a volume constante. Então você já sabe, vamos usar
Como o gás é monoatômico e se trata de um mol de gás:
Então:
: Processo isotérmico..
De novo, como é um processo isotérmico:
Processo isovolumétrico. .
Novamente, usando
Passo 4
Vamos olhar para o trabalho total. Se ele for negativo, é um refrigerador, se for positivo, é uma maquina térmica.
Então:
Como . O quociente acima vai dar um numero menor que 1. Então:
Mas, como , , então:
Show? Agora olhe o gráfico... é maior que . Então, o trabalho total é positivo.
Logo, o ciclo representa uma máquina térmica!!!
Resposta
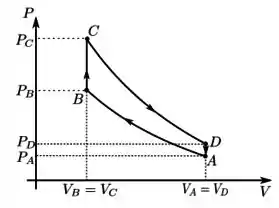
; ; ;
; ; ;
Logo, o ciclo representa uma máquina térmica!!!