Uma amostra com de um gás ideal diatômico, , é submetida a um processo cíclico, Inicialmente, , o gás ocupa um volume de à temperatura de e então é comprimido adiabaticamente até atingir o volume de , ponto . Em seguida, o gás é aquecido a pressão constante até retornar ao volume inicial, . Finalmente o gás retorna ao ponto em um processo no qual o volume é mantido constante.
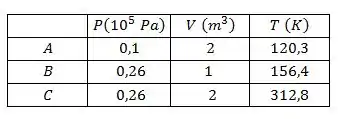
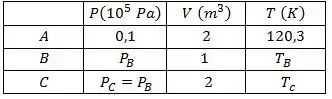
Determine os valores de pressão, volume e temperatura remanescentes nos pontos completando a tabela a seguir.
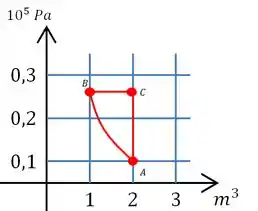
Faça um esboço do processo no plano .
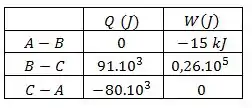
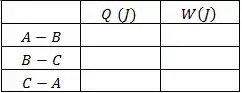
Preencha a tabela com os valores determinados para o calor trocado e o trabalho realizado em cada trecho do processo cíclico, tomando os sinais positivos como os correspondentes a calor recebido e a trabalho realizado pelo gás e negativos em casos opostos.
Qual é a eficiência de uma máquina térmica que opere com esse processo cíclico?
Passo 1
Alguns valores foram dados pelo enunciado já, então não precisamos nem fazer conta.
O volume em foi dado e é e o em também, já que ele volta ao volume inicial. E como o processo é isobárico então . Então nossa tabela já está assim:
Vamos agora estudar o processo que é adiabático, então e
Como não temos informação sobre o trabalho nem variação de energia interna. Vamos usar a relação
Como a constante é
E existe uma relação entre e :
Assim, a nossa constante vale:
Sabendo o valor de , podemos usar a relação que terminamos de falar
Então vamos descobrir
Agora, podemos usar o “PiViTi-PoVoTo”:
Para completar a tabela falta apenas encontrarmos o valor de , porque já encontramos
E para descobrirmos a temperatura em , vamos usar “PiViTi-PoVoTo”, novamente.
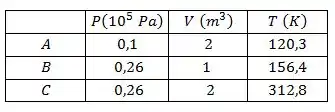
E assim completamos nossa tabela
Passo 2
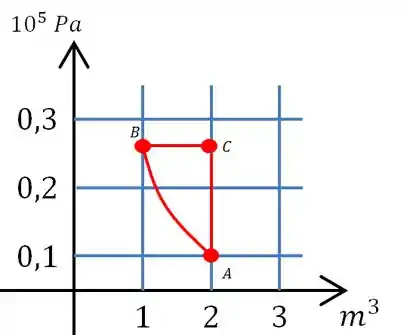
Vamos desenhar um gráfico então
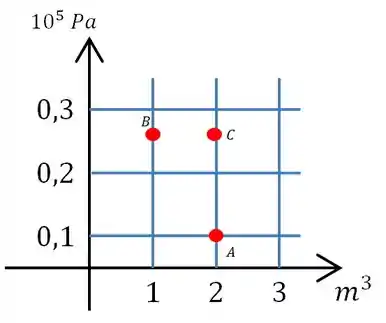
Em vermelho está os estados e , falta agora só fazermos o curva que representa o processo de um estado para o outro.
Do estado para temos um processo adiabático então a curva no gráfico é uma hipérbole. E o processo é a pressão constante então é uma reta horizontal e o processo é isovolumétrico então é uma reta vertical.
Desta forma, o gráfico fica assim:
Passo 3
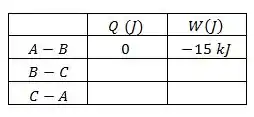
Agora vamos utilizar a primeira lei da termodinâmica para conseguirmos completar essa outra tabela.
O primeiro processo é que é adiabático então e
Como a variação da energia interna é dada por:
Como o gás é diatômico, , o número de mols foi dado . O valor da constante é .
Como o trabalho é , então
A primeira linha da tabela está completa.
Passo 4
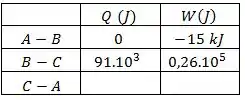
Agora vamos analisar o processo que isobárico, em um processo a pressão constante o trabalho é dado:
E o Calor trocado é
No primeiro passo já vimos que
E assim completamos a segunda linha da tabela
Passo 5
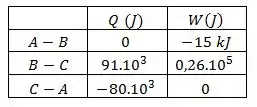
Por último analisaremos o processo , por ser um processo a volume constante. O trabalho é zero por não ter variação de volume.
E o calor trocado é dado por:
Por fim, completamos a tabela
Passo 6
A fórmula do rendimento é dada por
O trabalho do ciclo é só somarmos com e
E o é o calor recebido pelo ciclo, assim o rendimento é:
Resposta