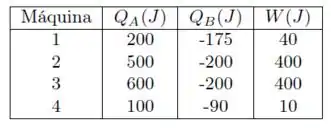
Um youtuber diz ter inventado 4 máquinas. Todas operam entre os mesmos 2 reservatórios de calor, a e a . O calor trocado por cada máquina com o reservatório a temperatura alta () e com o reservatório a temperatura baixa () e o trabalho realizado () por cada máquina em um ciclo são:
Considere as seguintes afirmações sobre a violação da Primeira e da Segunda Leis da Termodinâmica:
(I) Apenas as máquinas 1 e 2 violam a 1ª Lei.
(II) Apenas as máquinas 2 e 3 violam a 2ª Lei.
(III) Apenas a máquina 2 viola a 2ª Lei.
(IV) Apenas a máquina 4 viola a 2ª Lei.
(V) Apenas a máquina 3 é viável.
Estão corretas:
(a) Apenas as afirmativas I e II.
(b) Apenas as afirmativas I e V.
(c) Apenas as afirmativas IV e V.
(d) Apenas as afirmativas I e III.
Passo 1
Opa!! Vamos analisar primeiro em relação a primeira lei.
Ela diz pra gente que
Mas como uma máquina opera em ciclos.
Com isso
Esse , ou seja, o calor fornecido pela fonte quente e o calor fornecido para a fonte fria.
Então
Esse , tá em módulo, ok?! Tem esse menos na frente pra justamente mostrar que ele tá sendo retirado da máquina para o reservatório frio, ele tá saindo do sistema. Ok?
Agora, é só verificarmos quais máquinas satisfazem essa equação, que aí elas vão satisfazer a primeira lei.
Máquina 1:
Opa! Essa não satisfaz a primeira lei.
Máquina 2:
Opa! Essa não satisfaz a primeira lei.
Máquina 3:
Uhul! Essa satisfaz a primeira lei.
Máquina 4:
Uhul! Essa também satisfaz a primeira lei.
Com isso, vemos que a afirmativa (I) Apenas as máquinas 1 e 2 violam a 1ª Lei. Está correta.
Passo 2
Vamos analisar a segunda lei agora.
Pela 2ª lei da Termodinâmica, nenhuma máquina térmica pode apresentar um rendimento de Ou seja, ela precisa dissipar uma parte de energia. E além disso, a máquina térmica ideal, com o maior rendimento, seria a máquina de Carnot. Que como eu disse, é ideal. Ela não existe, mas representa a maior eficiência de uma máquina. Então, a eficiência de máquinas reais são sempre menores que a eficiência de Carnot. Vamos analisar essa condição agora.
Então, se uma máquina tiver rendimento melhor do que a de Carnot, ela tá violando a segunda lei, ok?
Vamos calcular a eficiência das máquinas.
Para a máquina 1:
Portanto, essa satisfaz a segunda lei.
Para a máquina 2:
Portanto, essa não satisfaz a segunda lei.
Para a máquina 3:
Portanto, essa não satisfaz a segunda lei.
Para a máquina 4:
Portanto, essa satisfaz a segunda lei.
Assim, as máquinas 2 e 3 violam a segunda lei.
Então a alternativa correta é a letra a).
Resposta
Letra a)