Uma máquina térmica funciona com um gás ideal diatômico segundo um ciclo de Diesel( diagrama pV mostrado na figura abaixo, onde as transformações são adiabáticas). Considere que a pressão, o volume a temperatura do gás em são , respectivamente.
Considere e
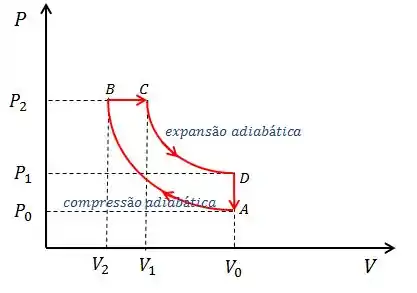
- Encontre as pressões , em função de
- Determine as temperaturas do gás nos estados respectivamente em função de
- Obtenha em função de , o calor trocado entre o gás e as vizinhanças nos processos Diga qual foi o sentido da troca de calor em cada processo.
- Calcule, em função de , o trabalho total realizado pelo ciclo.
- Obtenha o rendimento da máquina que opera segundo esse ciclo.
Passo 1
a)
Pra achar , basta a gente aplicar a fórmula:
Como o gás é diatômico:
E:
Assim:
A pressão no ponto é a mesma que . A partir do ponto , ocorre uma expansão adiabática até o ponto , que possui a nossa querida pressão . O volume de é o e o de o
Assim:
Assim:
Passo 2
b)
Pra achar , vamos usar a equação dos gases:
Como:
Então:
Podemos achar usando:
Assim:
Como:
Então:
Pra achar , vamos usar novamente a equação dos gases:
Assim:
Passo 3
c)
O calor trocado em é dado à pressão constante, então usaremos na fórmula:
Assim:
Como o calor é positivo, o calor está sendo transferido do ambiente para o gás.
O calor trocado em é feito à volume constante. Assim:
Como o calor é menor que zero, o calor tá sendo transferido do sistema para o ambiente. Assim, o sistema está perdendo calor.
Passo 4
d)
Como a variação de energia interna de um ciclo é nula:
O calor do ciclo é a soma daqueles calores calculados antes:
Assim:
Como:
Então:
Passo 5
e)
Pelo sentido desse ciclo, o ciclo representa uma máquina térmica. Assim o rendimento é dado por:
O calor é absorvido onde o calor é positivo, assim, em
Assim:
Resposta
a)
b)
c)
O calor está sendo transferido do ambiente para o gás.
O calor tá sendo transferido do sistema para o ambiente.
d)
e)