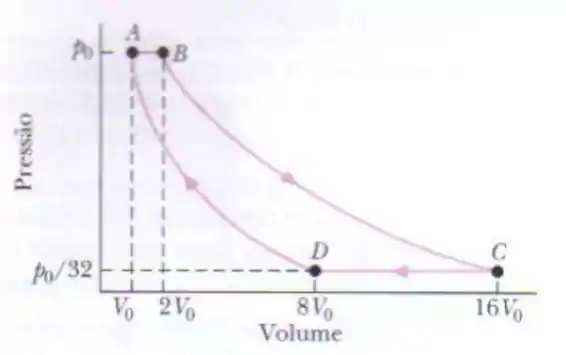
Um gás ideal é a substância de trabalho em uma máquina térmica que descreve o ciclo mostrado na figura abaixo. Os processos e são reversíveis e adiabáticos. O gás é monoatômico, diatômico ou poliatômico? Qual é a eficiencia da máquina?
Passo 1
Temos que descobrir se o gás é monoatômico, diatômico ou poliatômico.
Para isso podemos analisar tanto o processo ou , nós vamos escolher analisar o processo .
Como o enunciado disse, é um processo adiabático. Então podemos usar a relação
Então no processo , temos que
O gráfico nos fornece o dado de pressão e volume nos estados e , substituindo na equação temos
Cortando os termos em cumun
Se lembrarmos da tabela que fizemos em uma das teorias anteriores, onde relacionamos com o grau de liberdade.
Assim, sabemos que se
Então o gás é monoatômico
Passo 2
Para calcular a eficiência da máquina vamos usar a fórmula que aprendemos
Como os processo e são adiabáticos isso significa que não há troca de calor nesses processo assim, sabemos que só há troca de calor nos processos e .
Sendo que no processo o sistema absorve energia, então é aqui que vamos calcular o , através da fórmula a seguir por ser um processo a pressão constante
Como o gás é monoatômico, temos que
Por “piviti-povotó” temos que
Como em , a pressão é constante, teremos:
Como :
Substituindo esse valores na fórmula de e o valor de e que temos no grágico, chegamos em
Pela equação geral dos gás temos que
Substituindo na equação de
O que vale
Passo 3
Agora no processo é onde o sistema vai liberar calor, sendo assim vamos calcular o
Assim como fizemos no processo , usando “piviti-povotó" temos que:
Como :
Assim,
Porém não sabemos o valor de , novamente vamos usar “piviti-povotó” para acharmos uma relação entre e , analisando o processo
Substituindo pelos valores do gráfico temos
Assim
Substituindo na equação de
Lembrando que
Chegaos em:
Passo 4
Agora que temos uma equação para e , vamos substituir na fórmula de rendimento da máquina térmica
Resposta
Monoatômico