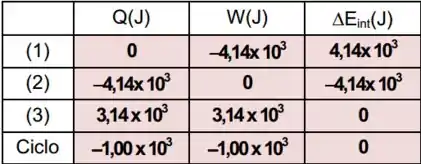
A figura abaixo mostra um cilindro contendo um mol do gás nitrogênio (), fechado por um pistão móvel e submerso numa mistura de gelo com água (). O gás sofre as seguintes transformações (diagrama ao lado da figura):
(1) O pistão, inicialmente na posição , é empurrado rapidamente para baixo, até a posição (processo adiabático), comprimindo o gás até ;(2) É, então, mantido na posição até que o gás esteja novamente na temperatura da mistura gelo-água (considere este processo como reversível isovolumétrico).(3) Em seguida, o pistão é erguido lentamente de volta à posição (processo isotérmico).
Observa-se que de gelo são derretidos durante o ciclo. (Calor de fusão do gelo ).
Dados:
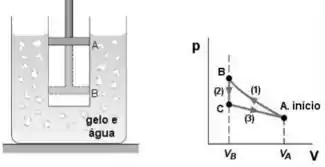
Tabela:

- Calcule o calor trocado entre o gás e a mistura gelo-água durante o ciclo. Obtenha o trabalho realizado sobre o gás durante o ciclo e complete a última linha da tabela acima.
- Calcule o trabalho realizado pelo gás na etapa (3) e complete, na tabela, a linha correspondente a essa etapa.
- Obtenha o trabalho realizado sobre o gás na etapa (2) e coloque o valor na tabela. Em seguida, calcule o trabalho na etapa (1) e complete a linha (1) da tabela.
- Calcule o calor cedido pelo gás na etapa (2) e Complete a linha (2) da tabela.
Passo 1
a):
Precisamos calcular:
- O calor trocado entre o gelo e o gás.
- O trabalho realizado pelo gás.
- E a energia interna, que é o que precisamos por na ultima linha.
Pra calcular o calor trocado, é só a gente calcular o calor recebido pelo gelo, certo?
Porque, afinal de contas, o calor cedido pelo gás no ciclo tem que ser igual ao calor recebido pelo gelo, já que a energia sempre se conserva. Pegou o bizu?
Mas, precisamos lembrar de trocar o sinal. Como o calor é recebido pelo gelo, esse é positivo. O calor cedido pelo gás tem que ser negativo:
Assim, o calor cedido é:
Passo 2
Como num ciclo a variação da energia interna é zero, pela primeira lei:
Além disso, como acabamos de falar, a informação que falta na tabela é:
Passo 3
b):
É o trabalho de uma transformação isotérmica. Então vamos usar aquela velha integral:
Como:
Como :
Como:
Como a transformação de 3 é isotérmica:
Passo 4
c):
trabalho realizado em 2 é igual a zero, á que a variação de volume é nula:
Assim:
Agora, pra achar o trabalho de 1, fica muito mais fácil usar o trabalho total do que ficar fazendo contas diretamente:
Como o trabalho total é a soma dos trabalhos:
Trabalho 3 foi calculado no item anterior e
Precisamos calcular a variação da energia interna de 1:
Como é um processo adiabático:
Passo 5
d):
Vamos usar o mesmo principio do trabalho total, agora com o calor total:
Bom, o calor de 1 é nulo, já que é uma transformação adiabática:
E como a transformação de 3 é isotérmica:
Então:
Lembrando que em
Então:
Resposta
a):
b):
c):
d):
TABELA: