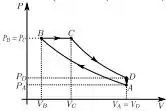
Um mol de gás ideal, com calor específico molar a volume constante , é submetido à seguinte sequência de processos REVERSÍVEIS:
• Compressão adiabática do estado inicial para o estado;
• Expansão isobárica do estado ao estado ;
• Expansão adiabática do estado ao estado ;
• Diminuição de pressão, a volume constante, do estado ao estado .
1. Desenhe o diagrama PV do ciclo ESPECIFICANDO AS CURVAS CORRESPONDENTES A CADA ETAPA E A ORIENTAÇÃO DO CICLO.
2. Calcule o calor trocado (INDICANDO SE FOI ABSORVIDO OU CEDIDO) pelo sistema em cada etapa em termos das temperaturas nos estados , , e , de e, se necessário, da constante universal dos gases.
3. Calcule o trabalho realizado pelo sistema em cada etapa, em termos das mesmas variáveis.
4. Este ciclo descreve um motor ou um refrigerador? Calcule o rendimento, caso seja um motor, ou o coeficiente de desempenho , caso seja um refrigerador, em termos das mesmas quantidades do item anterior.
Passo 1
- Como se trata de um gás ideal as curvas adiabáticas são do tipo , onde .
- Nas etapas adiabáticas o calor trocado é nulo, por definição. Logo, .
- Trabalho:
- Trata-se de um motor térmico, pois o sistema realiza trabalho.
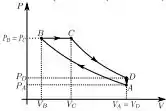
Passo 2
A etapa é isobárica, logo o calor pode ser escrito como . ABSORVIDO.
A etapa é isocórica, logo o calor pode ser escrito como , mas como temos a diminuição da pressão, também teremos a diminuição da temperatura, então: . CEDIDO.
Passo 3
Etapa : Adiabática: ,
Etapa : Isobárica: ,
Etapa : Adiabática:,
Etapa: Isocórica:
Passo 4
O rendimento pode ser escrito como:
Resposta
. Absorvido
. Cedido.