Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 34.
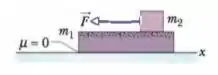
(Cap 6 – Ex 34) Na Fig. 6-37, uma prancha de massa repousa em um piso sem atrito e um bloco de massa repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é e o coeficiente de atrito cinético é . O bloco é puxado por uma força horizontal de módulo . Em termos dos vetores unitários, qual é a aceleração (a) do bloco e (b) da prancha?
Passo 1
Falaiii galerinha do responde ai, tudo certinho?
Bora para mais uma?
Vamos iniciar essa questão fazendo o DCL para cada um dos blocos:
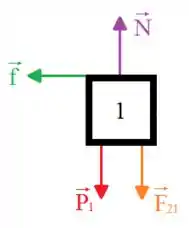
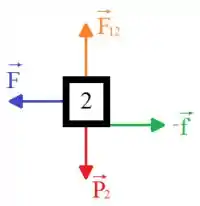
A partir dessa ilustração fica mais fácil aplicar a segunda lei de Newton nos blocos. Para tanto, vamos iniciar aplicando a segunda lei de Newton aos eixos e do bloco :
Consideramos o eixo em equilíbrio, pois o movimento ocorre exclusivamente no eixo .
De maneira análoga, vamos aplicar a segunda lei de Newton para o bloco :
Obs: os sinais negativos expostos do lado direito das igualdades é representando que estamos supondo que o movimento ocorre para a esquerda nos dois casos, no sentido negativo do eixo . Caso essa suposição não seja verdadeira, encontraremos a aceleração com valor negativo.
Lembrando que podemos determinar a força de atrito estático máximo e a força de atrito cinético a partir da seguinte relação:
Para determinar a força de atrito estático máximo, devemos usar o coeficiente de atrito estático, , e para determinar a força de atrito cinético, usamos o coeficiente de atrito cinético, .
Passo 2
Vamos começar determinando o valor da força de atrito estático máximo:
Neste caso, devemos perceber que . Para tanto, vamos determinar o usando a :
Assim, substituindo essa expressão na equação de :
Passo 3
No caso do bloco não deslizar sobre a prancha, , assim, podemos resolver o sistema envolvendo a e a para analisar se , caso isso seja falso, então o bloco desliza sobre a prancha. Iniciando, isolando o na :
Substituindo essa expressão na :
Isolando :
Como , então o bloco desliza sobre a prancha. Por isso, devemos usar a força de atrito cinético e as acelerações do bloco e da prancha não serão iguais.
Passo 4
Isolando na :
Lembrando que :
Portanto, a aceleração do bloco em termos dos vetores unitários será:
Passo 5
Para determinar a aceleração , faremos de maneira análoga ao passo anterior, porém usaremos a :
A aceleração da prancha, portanto, será:
Resposta
- ;
- .