Halliday - Vol.1 - Ed. 8 - Capítulo 5 – Problemas Adicionais – Questão 73
(Capítulo 5 – Problemas Adicionais – Exercício 73) Um operário arrasta um caixote no piso de uma fábrica puxando-o por uma corda. O operário exerce uma força de módulo sobre a corda, que está inclinada de um ângulo em relação à horizontal, e o chão exerce uma força horizontal de módulo que se opõe ao movimento. Calcule o módulo da aceleração do caixote (a) se a massa do caixote é e (b) se o peso do caixote é .
Passo 1
E aíí turma, vamos lá pra mais uma!
Vamos iniciar fazendo o diagrama de corpo livre para visualizarmos como as forças estão dispostas:
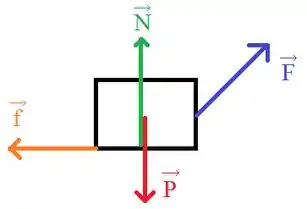
A partir desta ilustração podemos escrever a segunda lei de Newton para a componente na direção do movimento:
Isolando :
Passo 2
a) Substituindo os valores para o primeiro caso, em que a massa é :
Passo 3
b) Substituindo agora para o segundo caso, em que o peso é , temos que a massa será
Então, substituindo na expressão do passo 1:
E arrasamosss
Resposta
- ;
- .