Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 17.
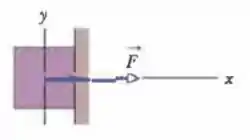
(Cap 6 – Ex 17) Uma força horizontal de empurra um bloco de de peso contra uma parede vertical (Fig. 6-26). O coeficiente de atrito estático entre a parede e o bloco é e o coeficiente de atrito cinético é . Suponha que o bloco não esteja se movendo inicialmente. (a) O bloco vai se mover? (b) Qual é a força que a parede exerce sobre o bloco em termos dos vetores unitários?
Passo 1
Fala galerinha bonita, tudo joinha?!!
Para determinar se o bloco vai se mover ou não, precisamos comparar se o peso da caixa é superior a força de atrito estático máximo. Sabendo que, para determinar o módulo desta força, podemos usar a seguinte relação:
Portanto, devemos determinar a normal inicialmente.
Passo 2
Aplicando a segunda lei de Newton para o eixo :
Como não há movimento no eixo :
Isolando e substituindo o valor de :
Passo 3
Com a normal calculada, podemos usar a para determinar o módulo da força de atrito máximo:
No eixo só temos o peso (vertical para baixo) e o atrito (vertical para cima), como o peso tem módulo menor do que , ou seja:
Então, o bloco não irá se mover e a força de atrito estático que atua sobre o bloco terá módulo igual ao módulo do peso para garantir o equilíbrio.
Passo 4
Sabendo o módulo da força de atrito e da normal, podemos escrever essas duas forças em termos dos vetores unitários, tendo em vista que são estas forças que a parede exerce sobre o bloco. Assim:
Resposta
- ;
- .