Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 9.
(Cap 6 – Ex 9 ) Um bloco de está inicialmente em repouso em uma superfície horizontal. Uma força horizontal de módulo e uma força verticalsão aplicadas ao bloco Os coeficientes de atrito entre o bloco e a superfície são e. Determine o módulo da força de atrito que age sobre o bloco se o módulo de é (a) (b) e (c)
Passo 1
Eai galerinha bonita, tudo bem?
Bora desenrolar essa comigo?
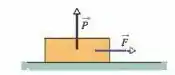
Show de bolinhas pessoal, temos uma força de e uma força , perpendicular a superfície que não sabemos o módulo, atuando sobre um bloco de massa . E sabendo que os coeficientes de atrito estático e cinético são respectivamente e , o enunciado nos pede pra determinar o módulo da força de atrito pra alguns casos.
Então beleza, a força é a força que modificará o movimento no eixo , a força irá mudar o módulo da força normal pois ao invés de , com essa força atuando temos que e isolando a normal temos que:
Passo 2
Sabendo como calcular a normal podemos chegar na força de atrito em (a), já que , portanto temos que:
Calculando
Chegamos em uma maior que os , assim, o corpo estará em repouso.
Passo 3
Para (b) fazemos o mesmo processo para chegar em .
Calculando
Chegamos em uma menor que os , assim, o corpo se movimentará e a real força de atrito é calculada com , sua nova é :
Passo 4
Em (c) novamente temos o mesmo processo:
Já sabemos que sobre essas condições o corpo irá se mover então vamos calcular diretamente com .
Resposta
- (b) (c)