Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 16.
(Cap 6 – Ex 16) Você depõe como perito em um caso envolvendo um acidente no qual o carro bateu na traseira de um carro que estava parado em um sinal vermelho no meio de uma ladeira (Fig. 6-25). Você descobre que a inclinação da ladeira é , que os carros estavam separados por uma distância quando o motorista do carro freou bruscamente, bloqueando as rodas (o carro não dispunha de freios ABS), e que a velocidade do carro no momento em que o motorista pisou no freio era . Com que velocidade o carro bateu no carro se o coeficiente de atrito cinético era (a) 0,60 (estrada seca) e (b) (estrada coberta de folhas molhadas)
Passo 1
Falaiii galerinha do responde ai, tudo certinho?
Bora para mais uma?
Para iniciar esta questão, vamos visualizar o DCL do carro :
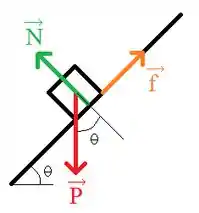
A partir dele, podemos aplicarr a segunda lei de Newton para cada eixo do carro :
Lembrando que para calcular o módulo da força de atrito cinético podemos usar a seguinte relação:
Como desejamos determinar a aceleração do carro para em seguida aplicar a equação de Torricelli para determinar a velocidade do carro no momento da colisão, então iremos usar a , porém para a aceleração ser a única incógnita de nossa equação, vamos ter que usar a para definir a normal e substituir na . Com a força de atrito calculada, conseguimos determinar a aceleração .
Passo 2
Vamos usar a para determinar o módulo da força normal:
Como não há movimento no eixo , então :
Isolando o :
Passo 3
Escrevendo a da força de atrito cinétio usando a :
Passo 4
Agora, vamos usar a para definir a aceleração do carro:
Dividindo os dois lados da equação por :
Substituindo os valores para os dois casos:
O sinal negativo que apareceu no nos afirma que supomos o sentido errado quando escrevemos a segunda lei de Newton, portanto, mesmo com o carro com o freio acionado, ele está acelerado.
Passo 5
Por fim, com os valores da aceleração em mãos, vamos aplicar Torricelli para cada caso:
Portanto, as respectivas velocidade de colisão são e .
Resposta
- ;
- .