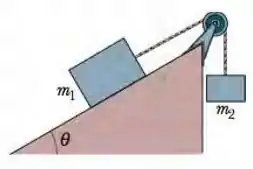
(Capítulo 5.9 – Exercício 59) Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig. 5-52). Quais são (a) o módulo da aceleração de cada bloco, (b) o sentido da aceleração do bloco que está pendurado e (c) a tensão da corda?
Passo 1
Fala aii galerinha do RespondeAí, tudo beleza??
Como temos duas massas conectadas através de um cabo sobre uma rampa, este será um problema de aplicação da segunda lei de Newton (), usando também o conceito da terceira lei de Newton (ação e reação).
Para questões como essa, é bastante interessante sempre fazer o esboço das forças que atuam em cada corpo:
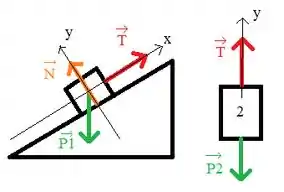
Além disso, é importante lembrar que como a polia é ideal as tensões no bloco e são iguais.
Os blocos se movimentam em conjunto então ambos têm a mesma aceleração ok?
Sabemos que os dois blocos têm em comum duas coisas: a aceleração e a tração. vamos trabalhar em cima dessas informações
Passo 2
Vamos começar escrevendo a segunda lei de Newton para o eixo do bloco . Não sabemos se o bloco 1 vai subir ou descer o plano inclinado por isso, vamos supor que o bloco suba o plano inclinado, caso essa afirmação seja falsa, o módulo da aceleração que encontraremos será negativo.
Segunda lei de Newton para o eixo x:
Substituindo os valores conhecidos e isolando o :
Logo:
Não sabemos ainda o valor da aceleração , então vamos guardar essa equação de em função de .
Passo 3
Agora vamos fazer a mesma coisa para o eixo do bloco , lembrando que, como consideramos que o bloco está subindo, então o bloco está descendo e, por isso, a aceleração é negativa. Assim:
Isolando o e substituindo os valores conhecidos:
Achamos outra equação de em função de .
Passo 4
Conseguimos achar duas equações que relacionam e , que são iguais em ambos os blocos. Então se a gente igualar as duas, vamos ter que:
Isolando o :
Como, encontramos a aceleração positiva, então nossa suposição foi correta e, portanto, o bloco está acelerado para baixo.
Passo 5
Para achar a tensão na corda, podemos usar qualquer uma das equações. Nessa solução vamos usar a segunda equação que encontramos no passo 3
E arrasamos!!
Resposta
- ;
- ;
- .