Halliday - Vol.1 - Ed. 8 - Capítulo 5 – Seção 9 – Questão 37
(Capítulo 5.9 – Exercício 37) Uma esfera com uma massa de está suspensa por uma corda. Uma brisa horizontal constante empurra a esfera de tal forma que a corda faz um ângulo de com a vertical. Determine (a) a força da brisa sobre a bola e (b) a tensão da corda.
Passo 1
Show de belezeras galerinha, pra gente começar essa questão, precisamos ter em mente o que o enunciado nos dá, então saca só.
O enunciado começa dizendo que a massa da esfera presa numa corda é dada como:
Ele continua falando que uma brisa empurra a esfera de forma que a corda faz um ângulo com a vertical e, a partir disso, pede para determinar a força da brisa sobre a bola e a tensão na corda.
Passo 2
Iradoso, então vamos fazer o diagrama de corpo livre da esfera para podermos entender melhor:
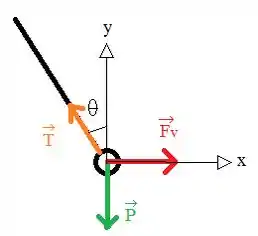
Vamos escrever a segunda lei de Newton para o eixo :
Como a bola está em equilíbrio, então:
Deixa essa equação guardada aí, beleza?
Passo 3
b) Vamos escrever agora a segunda lei de Newton para o eixo :
Como a bola está em equilíbrio:
Substituindo os valores:
Passo 4
a) Com o valor de calculado, podemos determinar usando a , tal que:
Logo:
Sucesso demais!!
Resposta
;
.