(Capítulo 5.9 – Exercício 18) Tarzan, que pesa , salta de um rochedo na ponta de um cipó de que está preso ao galho de uma árvore e faz inicialmente um ângulo de com a vertical. Suponha que um eixo é traçado horizontalmente a partir da borda do rochedo e que um eixo é traçado verticalmente para cima. Imediatamente após Tarzan pular da encosta, a tensão do cipó é . Nesse instante, quais são (a) a força do cipó sobre Tarzan em termos dos vetores unitários, a força resultante sobre Tarzan (b) em termos dos vetores unitários e como (c) módulo e (d) ângulo em relação ao sentido positivo do eixo . Quais são (e) o módulo e (f) o ângulo da aceleração de Tarzan nesse instante?
Passo 1
E aíí parsa, tudo certinho??
Boraaa falar sobre o Tarzan :P esse exercício nos dá o peso dele:
O tamanho do cipó:
O ângulo inicial que o cipó faz com a vertical:
E o módulo da tensão no cipó após o pulo:
A partir daí, o problema nos pede a força do cipó sobre o Tarzan em termos dos vetores unitários (), a força resultante sobre o Tarzan (), o módulo e o ângulo em relação ao semieixo positivo desta força resultante ( e ), e o módulo e o ângulo da aceleração do Tarzan neste instante ( e ).
Passo 2
Vamos começar visualizando as forças que agem sobre o Tarzan no imeditamente após ao pulo:
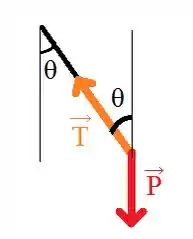
Por trigonometria, podemos escrever o vetor em função das componentes, considerando o semieixo positivo para direita e o semieixo positivo para cima:
Substituindo os valores:
Passo 3
No Tarzan, só age sobre ele a força peso e a força da tração da corda, como mostra a ilustração do passo anterior, assim, podemos escrever a força peso em termos dos vetores unitários e fazer o somatório vetorial com a tração para determinar o vetor força resultante:
Fazendo a soma vetorial:
Somando as componentes, eixo por eixo:
Passo 4
Para calcular o módulo da força resultante sobre o Tarzan vamos usar a equação explicitada no passo inicial, show? Se não, lembra, dá uma olhadinha lá rapidinho.
Passo 5
Para determinar o ângulo que este vetor faz com o semieixo positivo também usaremos também a equação dada no passo inicial:
Devemos tomar cuidado quando utilizando a função na calculadora, pois dois ângulos e possuem o valor. Assim, precisamos determinar em qual quadrante o nosso vetor está a partir da análise do sinal das componentes.
Como nosso vetor possui a componente e a componente negativas, então este só pode estar no terceiro quadrante, pois é o único cujo o seno e o cosseno são negativos, portanto:
Passo 6
Para determinar o módulo da aceleração, usaremos a segunda lei de Newton:
Porém, o problema nos deu somente o módulo do peso do Tarzan, para encontrar a massa devemos dividir o módulo do peso pela gravidade (), assim:
Isolando o :
Passo 7
Para determinar o módulo de faremos de maneira análoga ao que fizemos para a força resultante:
Passo 8
Para determinar o ângulo que a aceleração faz com o semieixo positivo, vamos lembrar da segunda lei de Newton:
A massa é uma grandeza escalar sempre maior que zero multiplicando o vetor, portanto, a aceleração terá sempre o mesmo sentido e a mesma aceleração da força resultando. Isso resulta que:
Resposta
- ;
- ;
- ;
- ;
- ;
- .