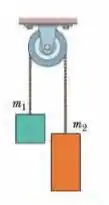
(Capítulo 5.9 – Exercício 55) A Fig. 5-47 mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa ; o outro tem massa . Quais são (a) o módulo da aceleração dos blocos e (b) a tensão da corda?
Passo 1
E aí galera, belezinha? Para fazer essa questão, vamos lembrar da equação da segunda lei de Newton:
Lembrando que esta definição pode ser utilizada em cada eixo separadamente:
Temos que notar que o módulo da tensão da corda no bloco é igual ao do bloco , porque a polia é ideal. Além disso, a aceleração das caixas também são iguais, porque o movimento de uma está ligada ao movimento da outra.
A partir dessas equações e interpretações podemos determinar a aceleração dos blocos e também a tensão na corda.
Bora!
Passo 2
Escrevendo a segunda lei de Newton para a componente do bloco :
Isolando o :
Escrevendo agora a segunda lei de Newton para a componente do bloco :
Obs: O sinal de menos do lado direito dessa equação é devido ter adotado que o bloco subiria, então este ficou com a aceleração positiva, enquanto o bloco descia, então este deve ficar com a aceleração negativa.
Isolando o :
Passo 3
Com as duas equações em mãos, vamos substituir a na para determinar a aceleração dos blocos:
Isolando :
Assim, substituindo os valores conhecidos:
Passo 4
Com a aceleração calculada, podemos substituir em qualquer das equações ( ou ) para determinar a tensão na corda:
Substituindo os valores conhecidos:
E é isso aíí
Resposta
- ;
- .