Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Atrito Estático + Atrito Cinético

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839404142434445

Enunciado

Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 3 - Problema 15.

(Cap 6 – Ex 15) O coeficiente de atrito estático entre o Teflon e ovos mexidos é cerca de 0,04 . Qual é o menor ângulo com a horizontal que faz com que os ovos deslizem no fundo de uma frigideira revestida com Teflon?

Passo 1

Faaaaaalaiiii, tudo na boaaa?

Belezera galerinha, se a gente fizer um desenho para o teflon e os ovos mexidos, teremos algo mais ou menos assim:

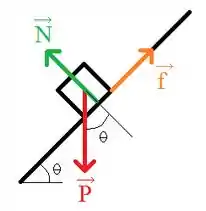
Nesse caso, podemos aproximar o formato dos ovos mexidos para um cubo (tenho talento pra culinária), enquanto a frigideira com teflon, assume a caracteristis de um plano inclinado.

Lembrando que a força de atrito estático máximo pode ser calculada através da seguinte relação:

f = μ s N

Passo 2

Iradoso, então escrevendo a segunda lei de Newton para o eixo perpendicular a trajetória, ou seja, na mesma direção da força normal (chamaremos por conveniência de eixo y ), obtemos:

N - P cos ⁡ θ = m a y

Como não há movimento no eixo y , então a aceleração é nula a y = 0 , de forma que:

N - P cos ⁡ θ = 0

Isolando N :

N = m g cos ⁡ θ

Passo 3

Com o valor da força normal calculada no passo anterior, vamos reescrever a equação da força de atrito, tal que:

f = μ s N

f = μ s   m g cos ⁡ θ

Passo 4

Agora escrevendo a segunda lei de Newton para o eixo x , ou seja, o eixo sobre o plano inclinado onde o ovo pode deslizar, temos que:

P sin ⁡ θ - f = m a x

Como estamos considerando que o ovo está na iminência do movimento, então a aceleração neste eixo também será nula a x = 0 , logo:

m g sin ⁡ θ - μ s   m g cos ⁡ θ = 0

Dividindo os dois lados da equação por m g :

sin ⁡ θ - μ s cos ⁡ θ = 0

sin ⁡ θ = μ s cos ⁡ θ

sin ⁡ θ cos ⁡ θ = μ s

Logo:

tan ⁡ θ = μ s

Isolando θ :

θ = tan - 1 ⁡ μ s

Substituindo os valores conhecidos:

θ = tan - 1 ⁡ ( 0,04 ) = 2,3 °

Resposta

θ = 2,3 °

Exercícios de Livros Relacionados

Na Fig. 6-37, uma prancha de massa m 1 = 40k g repousa em um piso sem atrito e um bloco de massa m 2 = 10k g repousa sobre a prancha. O coeficiente de atrito estático entre o bloco e a prancha é 0,60
Uma curva circular em uma rodovia é projetada para uma velocidade máxima de 60k m / h . Suponha que os carros não possuem sustentação negativa. (a) Se o raio da curva é 150m , qual é o ângulo de compe
A Fig. 6-20 mostra um bloco inicialmente estacionário de massa m sobre um piso. Uma força de módulo 0,500m g é aplicada com um ângulo θ =20 ° para cima. Qual é o módulo da aceleração do bloco se (a) μ
Um ciclista se move em um círculo de 25,0m de raio com uma velocidade constante de 9,00m / s . A massa do conjunto ciclista- bicicleta é 85,0k g . Calcule o módulo (a) da força de atrito que a pista e
Sam, com 75k g de massa, dispara com seus esquis a jato descendo uma rampa de 50m verticais de altura e 10 ° de inclinação. Os esquis desenvolvem um empuxo de 200N . Na base da rampa, Sam atinge uma v