Halliday - Vol.1 - Ed. 8 - Capítulo 5 – Seção 9 – Questão 50
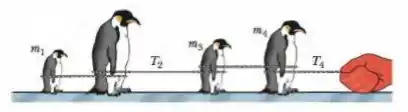
(Capítulo 5.9 - Exercício 50) A Fig. 5-49 mostra quatro pinguins que estão sendo puxados sobre gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e as tensões em duas das cordas são , , , e . Determine a massa do pinguim , que não é dada.
Passo 1
Belezera galerinha, esse é um tipo de questão conhecida como questão cascata, na qual a gente vai descobrindo um, substituindo no outro e no outro e no outro... haha então bora lá começar ela...
Para fazer esta questão, precisamos usar a segunda lei de Newton:
O enunciado nos dá três massas e duas tensões e nos pede o valor da massa .
Passo 2
Vamos iniciar essa questão considerando todos os pinguins como um sistema, assim teremos apenas uma força externa, a tensão . Escrevendo a segunda lei de Newton para esse sistema:
Substituindo os valores conhecidos:
Isolando o :
Passo 3
Vamos agora analisar o último pinguim. No eixo há somente uma tensão , portanto, escrevendo a segunda lei de Newton:
Como a aceleração do sistema é igual a aceleração individual de cada pinguim, então já temos a aceleração calculada em função de . Assim, substituindo os valores conhecidos:
Passo 4
Agora vamos aplicar a segunda lei de Newton para o pinguim que desejamos calcular a massa, lembrando que que atua no pinguim , também atua no pinguim (lembrar da terceira lei de Newton), portanto:
Substituindo os valores conhecidos e também a e , temos:
Passando o denominador da direita para o lado esquedo da igualdade:
Isolando :
E é isso aíí