Halliday - Vol.1 - Ed. 8 - Capítulo 5 – Seção 7 – Questão 15
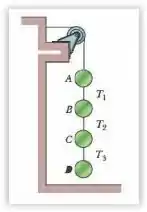
(Capítulo 5.7 – Exercício 15) A Fig. 5-33 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco , (b) do disco, (c) do disco C e (d) do disco?
Passo 1
Faaala galera, vamos lá falar mais sobre força e movimento 😉
Nesse exercício temos 4 discos ligados por cordas, sendo que lá em cima tem uma polia. Aí queremos encontrar as massas de cada um dos discos, sabendo que as tensões nas cordas são
Para encontrarmos essas massas, vamos usar o somatório de forças, que deve ser igual a 0 já que os discos estão em repouso
Bora!
Passo 2
Vamos começar pelo disco D, o que ta mais embaixo
Nele atuam a força peso e em sentidos contrários.
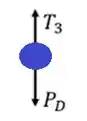
Como o somatório das forças é igual a zero podemos obter a seguinte equação:
Com isso podemos substituir os valores na equação para obter a massa do disco D:
Passo 3
Agora vamos para o disco C. As forças que atuam sobre ele são:
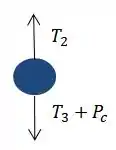
Novamente pelo somatório das forças igual a zero, podemos obter a seguinte equação :
Vamos substituir os valores que já temos na equação para obter a massa do disco C:
Passo 4
Vamos analisar as forças que atuam em B.
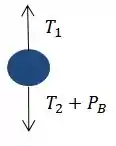
Como o somatório das forças é igual a zero podemos obter a seguinte equação:
Substituindo os valores que sabemos na equação para obter a massa do disco B:
Passo 5
Agora só falta o disco A.
Vamos analisar as forças:
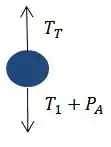
Sabendo que a força exercida na parede vale , essa vai ser a nossa tração total que está sendo exercida, usando o somatório de forças igual a zero teremos:
Substituindo os valores que sabemos na equação para obter a massa do disco A:
De boa pessoal?? Então partiu fazer mais exercícios!!!
Resposta
a)
b)
c)
d)