Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 6 – seção 5 - Problema 59.
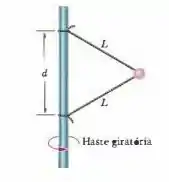
(Cap 6 – Ex 59) Na Fig. 6-45, uma bola de é ligada por meio de dois fios de massa desprezível, cada um com comprimento , a uma haste vertical giratória. Os fios estão amarrados à haste a uma distância um do outro e estão esticados. A tensão do fio de cima é . Determine (a) a tensão do fio de baixo; (b) o módulo da força resultante a que está sujeita a bola; (c) a velocidade escalar da bola; (d) a direção de
Passo 1
Falaiii meus queridos, tudo certinho?
Bora resolver essa comigoo?
A primeira coisa que devemos fazer é construir o diagrama de corpo livre da bola :
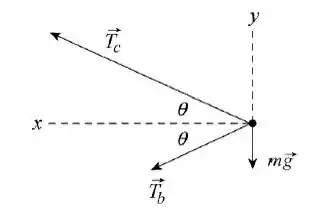
é a tensão exercida pelo fio de cima sobre a bola, é a tensão exercida pelo fio de baixo e é a massa da bola. Note que a tensão do fio de cima é maior que a do fio de baixo, porque precisa equilibrar, além da tensão do fio de baixo, o peso da bola.
Como de costume tomamos o eixo na direção do centro do movimento circular e o eixo para cima. Como o módulo da aceleração é , a Segunda Lei de Newton para o eixo nos dá :
em que é a velocidade da bola e é o raio do movimento circular.
A Segunda Lei de Newton para o eixo nos dá :
o que nos dá . Como o triângulo é equilátero, . Assim,
Até aqui beleza, galera ? Bora continuar então!
Passo 2
Nós sabemos que o módulo da força resultante é dado por :
Passo 3
Como de costume o raio do movimento circular é obtido através da relação:
Como , a velocidade da bola é dada por :
Passo 4
Bom galera , no movimento circular a direção de é sempre radial, para o centro do movimento circular.
Resposta
- A direção da força resultante será radialmente para dentro.
Atenção! Cientistas afirmam que o próximo exercício tem 117,3% de chances de cair na sua prova , não deixem de conferir