2) A figura abaixo mostra o gráfico de uma força que varia com a posição de uma partícula. Considere que a força é a força resultante que atua sobre a partícula.
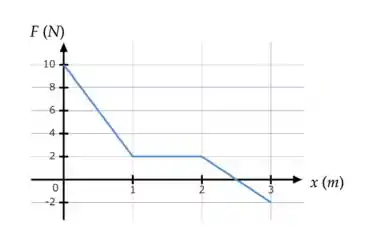
Ordene os trabalhos e realizados pela força nos deslocamentos , e , respectivamente; e os módulos , e das velocidades da partícula nas posições , e .
a) e
b) e
c) e
d) e
e) e
Passo 1
Fala aí, galerinha!!
Esse problema é para a gente usar a relação entre trabalho e o gráfico da função . A gente tem que:
Outra coisa que a gente vai usar é o teorema energia cinética – trabalho. Esse teorema nos diz que:
Usando essas informações a gente vai avaliar as grandezas que o problema nos pediu. Então vamos lá 😊
Passo 2
Vamos começar vendo como os trabalhos se comportam nos intervalos em que o enunciado nos fala. O primeiro deles é desde até . Olhando este intervalo, temos no gráfico um trapézio de base maior e base menor (vira a cabeça 90° para sua direita que você vê o trapézio!).
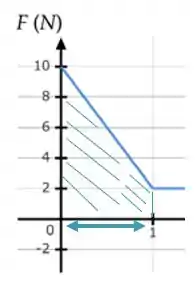
A altura deste trapézio é 1m (visto de lado), então temos a área dada por:
Para o segundo intervalo, até , temos, no gráfico um retângulo de altura e base indo de 1m até 2m, ou seja, a área é dada por:
E para o último intervalo, como temos uma parte que está em cima do gráfico e uma que está abaixo do gráfico, vamos separar esse trabalho em duas partes:
Na primeira parte temos um triângulo para cima então temos altura de 2N e base de m. O trabalho nesta parte é:
Para a segunda parte temos um triângulo para baixo, então teremos uma “área negativa”, na real é só o trabalho que vai ser negativo né. A altura desse triângulo é de 2N e a base é a mesma que antes. Ou seja:
Onde aquele sinal de menos a gente acrescentou por conta da figura estar para baixo do eixo . Dessa forma, o trabalho total neste intervalo é:
Então a ordem é:
Passo 3
Para estimar sobre as velocidades, vamos usar o teorema energia cinética – trabalho:
Vamos supor que a gente começa com uma velocidade inicial . O que acontece é que como o trabalho é positivo, ele aumenta a energia cinética do sistema, então a velocidade aumenta e temos uma velocidade no final desse trecho. Beleza?
No próximo trecho, vimos que também é positivo e de novo a energia cinética aumenta, então temos, ao fim desse trecho, uma velocidade .Por fim, a gente tem , isso significa que a energia cinética não se altera nesse trecho. Então teremos ao fim desse deslocamento.Juntando tudo temos:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
a) e