UFABC – Fenômenos Mecânicos – Lista 4 – Questão 05
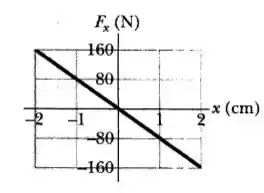
A fornece a força elástica em função da posição para o sistema massa mola. Puxamos o bloco até e o abandonamos. Qual é o trabalho realizado pela mola sobre o bloco ao se deslocar de para
(a) ,
(b),
(c) e
Passo 1
Oi, pessoal, tudo bem? Para resolver essa questão precisamos lembrar da fórmula do trabalho realizado por uma força do tipo :
E como calculamos a constante elástica? Como é uma equação do primeiro grau, a inclinação da reta que o representa corresponde à constante elástica .
O valor da constante elástica, ao analisarmos a figura fornecida pelo enunciado, é dado por pela razão da força pelo deslocamento:
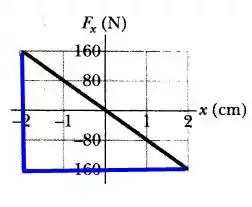
Beleza? Agora podemos aplicar a fórmula do trabalho para cada deslocamento pedido! Vamos lá?
Passo 2
Letra (a):
Quando o bloco é deslocado de para , temos:
Beleza?
Passo 3
Letra (b):
De forma análoga ao item anterior, quando o bloco é deslocado de para , temos:
Passo 4
Letra (c):
Quando o bloco é deslocado de para , por sua vez, temos que:
as posições são simétricas! Por isso o trabalho é nulo!
Passo 5
Letra (d):
Da mesma forma que nos itens anteriores, quando o bloco é deslocado de para , temos:
E é isso galera! Espero ter ajudado!