Uma força é aplicada ao longo de , essa força é variável. Podemos ver na figura abaixo a força ao longo dessa distância. Sabendo que o trabalho total é determine o valor de indicado no gráfico.
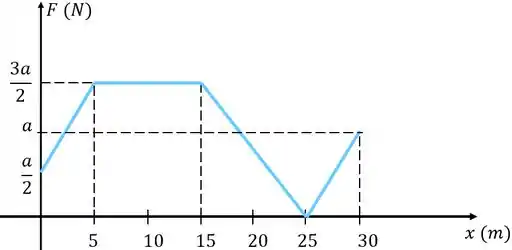
Passo 1
Para achar o trabalho vamos calcular a área do gráfico.
Podemos separar essa área em 4 partes para facilitar nossas contas
Passo 2
A área 1 é um trapézio, onde a base maior é a base menor é e a altura é .
Vamos ter
Passo 3
A área 2 é um retângulo de lados e . Então:
Passo 4
A área 3 é um triangulo, onde a base é e a altura é .
Vamos ter
Passo 5
A área 4 é um triangulo, onde a base é e a altura é 5.
Vamos ter
Passo 6
A área total via ser
Como essa área é o trabalho total
Resposta
Exercícios de Livros Relacionados
Um bloco de 5,0k g se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 7-38. A escala vertical do gráfico é d
Uma força F=c x -3,00 x 2 i → , onde F está em newtons, x em metros e e é uma constante, age sobre uma partícula que se desloca ao longo de um eixo x . Em x= 0 , a energia cinética da partícula é 20,0
Uma única força atua sobre um objeto de 3,0k g que se comporta como uma partícula, de tal forma que a posição do objeto em função do tempo é dada por x=3,0 t - 4,0 t 2+1,0 t 3 , com x em metros e t em
60. Uma partícula de massa m parte de x 0 = 0m com v 00m / s . Ao se mover para a direita sobre o eixo x , a partícula experimenta uma força variável dada por F x = F 0 sen ( c x ) , onde F 0 e c sã
Uma força de 160N estica 0,050m uma certa mola a partir do seu comprimento sem deformação. a) Qual é a força necessária para esticar essa mola 0,015m a partir do seu comprimento sem deformação? E para